Question

如图，AD∥BC，∠A=90°，E是AB上的一点，且AD=BE，∠1=∠2．

（1）△ADE与△BEC全等吗？请说明理由；
（2）若AD=3，AB=7，请求出△ECD的面积．

Answer 1

（1）全等；（2）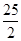

解析试题分析：（1）先根据等角对等边得到DE=EC，再结合平行线的性质即可证得结论；
（2）根据全等三角形的性质可得AE=BC，∠ADE=∠BEC，再根据勾股定理结合直角三角形的面积公式即可求得结果.
（1）∵∠1=∠2，
∴DE=EC．
∵AD∥BC，
∴∠B+∠A=180°．
又∵∠A=90°，
∴∠A=∠B=90°．
在Rt△ADE与Rt△BEC中，
∵DE=EC，AD=BE
∴△ADE≌△BEC（HL）；
（2）∵△ADE≌△BEC，
∴AE=BC，∠ADE=∠BEC．
∵AD=3，AB=7，
∴AE=BC=4．
∴DE=EC=5．
又∵∠ADE+∠AED=90°，
∴∠DEC=90°．
∴△DEC的面积为．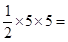
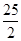考点：本题考查的是全等三角形判定和性质，勾股定理，三角形的面积公式
点评：解答本题的关键是熟练掌握两直线平行，同旁内角互补；全等三角形的对应边、对应角相等.