练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．已知$\root{3}{8-{x}^{2}}=8-{x}^{2}$，求x的值．

    分析 立方根等于本身的数有1、0、-1，故此可得到8-x2的值，从而可求得x的值．

    解答 解：∵立方根等于本身的数是1、0、-1，
    ∴8-x2=1或8-x2=0或8-x2=-1
    解得：x的值为±$\sqrt{7}$或±2$\sqrt{2}$或±3．

    点评 本题主要考查的是立方根、平方根的性质，熟练掌握相关性质是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    11．小明从如图所示的二次函数y=ax2+bx+c（a≠0）的图象中，观察得出了下面五条信息：①abc＞0；②a-b+c＜0；③b+2c＞0； ④a-2b+4c＞0；⑤2a=3b
    你认为其中正确信息的个数有（　　）
    A．2个B．3个C．4个D．5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．A、B两地相距6980000m，用科学记数法表示为（　　）m．
    A．69.8×105B．698×104C．0.96×107D．6.98×106

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

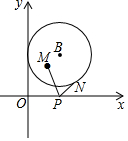    9．如图，平面直角坐标系中，已知点M（2，3）、以点B（3，4）为圆心，3为半径作⊙B，N是⊙B上的动点，P为x轴上的动点，则PM+PN的最小值为5$\sqrt{2}$-3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图，已知A，B两点的坐标分别为A（2$\sqrt{3}$，0），B（0，2），点P是△AOB外接圆上的一点，且∠AOP=45°．

    （1）如图1，求点P的坐标；
    （2）如图2，点Q是$\widehat{AP}$上一点，（不与A，P重合），连PQ，AQ，BQ，求$\frac{BQ-AQ}{PQ}$的值；
    （3）如图3，连BP，AP，在PB上任取一点，连AE，将线段AE绕A点顺时针旋转90°到AF，连BF，交AP于点G，当E在线段BP上运动时，（不与B，P重合），求$\frac{BE}{PG}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

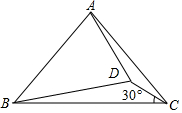    6．如图，在△ABC中，AB=AC，今在△ABC内部取一点D使得AB=BD=AC且∠DCB=30°，若CD=2且AC=2$\sqrt{37}$，试求△ABC面积（请详述理由）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．计算1+2-3-4+5+6-7-8+…-2015-2016=-2016．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

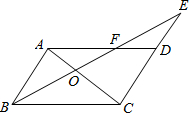    10．如图，?ABCD中，E为CD边的延长线上一点，BE交AD于F，AC交BF于点O．
    （1）已知：AB=4，BC=6，DE=$\frac{1}{2}$CD：①求DF的长；②求证：BF平分∠ABC．
    （2）求证：OB2=OE•OF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．惠民超市试销一种进价为每件60 元的服装，规定试销期间销售单价不低于进价，且获利不得高于40%．经试销发现，销售量y （件）与销售单价x （元）满足一次函数y=kx+b，且当x=70 时，y=50；当x=80 时，y=40．
    （1）求一次函数y=kx+b 的解析式；
    （2）设该超市获得的利润为W 元，试写出利润W 与销售单价x 之间的关系式；销售单价定为多少元时，超市可获得最大利润，最大利润是多少元？
    （3）若该超市预期的利润不低于500 元，试确定销售单价x 的取值范围．

    查看答案和解析>>

    同步练习册答案