解:(1)∵当x=0时,有最小值为1,
∴-

=0,

=1,
解得b=0,c=1,
∴抛物线关于y轴对称,
∵在直线y=2上截得的线段长为4,
∴抛物线经过点(-2,2)与(2,2),
∴4a+1=2,
解得a=

,
所以,此抛物线的解析式:y=

x
2+1;
(2)猜想:d
1=d
2.
设抛物线上的点P的坐标为(x,

x
2+1),
则d
1=

x
2+1,
d
2=PF=
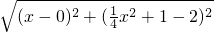
=

=

x
2+1,
所以,d
1=d
2;
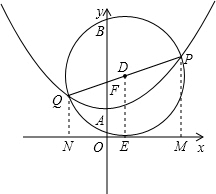
(3)①以PQ为直径的圆与x轴相切.
理由如下:过点P作PM⊥x轴于点M,过点Q作QN⊥x轴于点N,
由(2)可知,PF=PM,QF=QN,
∴PF+QF=PM+QN,
即PQ=PM+QN,
∵圆心D是直径PQ的中点,过D作DE⊥x轴于点E,
∴DE=

(PM+QN)=

PQ,
即圆心到x轴的距离等于圆的半径,
所以,以PQ为直径的圆与x轴相切;
②由切割线定理可得OE
2=OA•OB,
∵OA•OB=1,
∴OE
2=1,
解得OE=1,
设直线PQ的解析式为y=kx+2,
联立
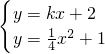
得,

x
2+1=kx+2,
整理得,x
2-4kx-4=0,
所以,线段PQ的中点横坐标为-
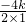
=2k,
即点E的坐标为(2k,0),
当点E在y轴右侧时,2k=1,
解得k=

,
此时,所求直线PQ对应的函数解析式为:y=

x+2,
当点E在y轴左侧时,2k=-1,
解得k=-

,
此时所求直线PQ对应的函数解析式为:y=-

x+2,
综上,所求直线PQ对应的函数解析式为:y=

x+2或y=-

x+2.
分析:(1)根据抛物线的顶点坐标列式求出b=0,c=1,再根据在直线y=2上截得的线段长为4,利用抛物线的对称性可得点(2,2)在抛物线上,然后把点的坐标代入抛物线解析式求出a的值,从而得解;
(2)设P点坐标为(x,y),根据两点间距离公式求出PF的长,即d
2,d
1等于P点的纵坐标的值;比较两距离即可;
(3)①过点P作PM⊥x轴于点M,过点Q作QN⊥x轴于点N,根据(2)的结论可得PF=PM,QF=QN,然后利用梯形的中位线定理可得圆心到x轴的距离等于PQ的一半,再根据直线与圆的位置关系判断圆与x轴相切;
②设圆与x轴的切点为E,根据切割线定理可得OE=1,再设直线PQ的解析式为y=kx+2,与抛物线解析式联立,根据点PQ的中点的横坐标的长度等于OE列式求出k值,即可得解.
点评:本题是二次函数的综合题型,其中涉及到的知识点有抛物线的顶点公式,抛物线的对称性,两点间的距离公式,梯形的中位线定理,直线与圆的位置关系的判定,圆的切割线定理,综合性较强,(3)要注意分情况讨论.

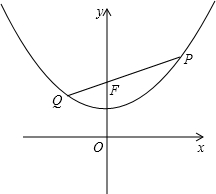 已知抛物线y=ax2+bx+c,当x=0时,有最小值为1;且在直线y=2上截得的线段长为4.
已知抛物线y=ax2+bx+c,当x=0时,有最小值为1;且在直线y=2上截得的线段长为4. =0,
=0, =1,
=1, ,
, x2+1;
x2+1; x2+1),
x2+1), x2+1,
x2+1,
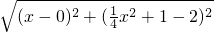 =
= =
= x2+1,
x2+1, (PM+QN)=
(PM+QN)= PQ,
PQ,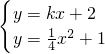 得,
得, x2+1=kx+2,
x2+1=kx+2,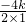 =2k,
=2k, ,
, x+2,
x+2, ,
, x+2,
x+2, x+2或y=-
x+2或y=- x+2.
x+2.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 与x轴的另一个交点为E.
与x轴的另一个交点为E. 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=