
【题目】在Rt△ABC中,∠ACB=90°,在斜边AB上分别截取AD=AC,BE=BC,DE=6,
点O是△CDE的外心,如图所示,则点O到△ABC的三边的距离之和是 . 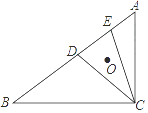
科目:初中数学 来源: 题型:
【题目】对代数式![]() ,老师要求任意取一个x的值后求出代数式的值.圆圆发现,大家所求得的代数式的值都大于等于0,即x=-3时代数式的最小值是0.利用这个发现,圆圆试着写出另外一些结论:①在x=-3时,代数式(x+3)2+2的最小值为2;②在a=-b时,代数式(a+b)2+m的最小值为m;③在c=-d时,代数式-(c+d)2+n的最大值为n;④在
,老师要求任意取一个x的值后求出代数式的值.圆圆发现,大家所求得的代数式的值都大于等于0,即x=-3时代数式的最小值是0.利用这个发现,圆圆试着写出另外一些结论:①在x=-3时,代数式(x+3)2+2的最小值为2;②在a=-b时,代数式(a+b)2+m的最小值为m;③在c=-d时,代数式-(c+d)2+n的最大值为n;④在![]() 时,代数式
时,代数式![]() 的最大值为29.其中正确的为( )
的最大值为29.其中正确的为( )
A. ①②③B. ①③C. ①④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作:在△ABC中,AC=BC=2,∠C=90°,将一块等腰直角三角板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点.图1,2,3是旋转三角板得到的图形中的3种情况.
研究:
(1)三角板绕点P旋转,观察线段PD和PE之间有什么数量关系,并结合图2加以证明;
(2)三角板绕点P旋转,△PBE是否能成为等腰三角形?若能,指出所有情况(即写出△PBE为等腰三角形时CE的长);若不能,请说明理由;
(3)若将三角板的直角顶点放在斜边AB上的M处,且AM:MB=1:3,和前面一样操作,试问线段MD和ME之间有什么数量关系?并结合图4加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明的爸爸骑着摩托车带着小明在公路上匀速行驶,小明每隔一段时间看到的里程碑上的数如下:12:00时是一个两位数,数字之和为7;13:00时十位与个位数字与12:00是所看到的正好互换了;14:00时比12:00时看到的两位数中间多出一个0.如果设小明在12:00看到的数的十位数字是x,个位数字是y,根据题意可列方程组为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知一个多边形的内角和是它的外角和的 3 倍,求这个多边形的边数.
(2)如图,点F 是△ABC 的边 BC 延长线上一点.DF⊥AB,∠A=30°,∠F=40°,求∠ACF 的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张去书店购买图书,看好书店有A,B,C三种不同价格的图书,分别是A种图书每本1元,B种图书每本2元,C种图书每本5元.
(1)若小张同时购买A,C两种不同图书的6本,用去18元,求购买两种图书的本数;
(2)若小张同时购买两种不同的图书10本,用去18元,请你设计他的购书方案;
(3)若小张同时购进A,B,C三种不同图书10本,用去18元,请你设计他的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图 1,在四边形 ABCD 中,AB∥DC,E 是 BC 中点,若 AE 是∠BAD 的平分线,试探究 AB,AD,DC 之间的数量关系,请直接写出结论,无需证明.
(2)如图 2,在四边形ABCD 中,AB∥DC,AF 与DC 的延长线交于点F,E 是BC 中点,若AE 是∠BAF 的平分线,试探究AB,AF,CF 之间的数量关系,证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在半径为6cm的⊙O中,点A是劣弧 ![]() 的中点,点D是优弧
的中点,点D是优弧 ![]() 上一点,且∠D=30下列四个结论:①OA⊥BC;②BC=
上一点,且∠D=30下列四个结论:①OA⊥BC;②BC= ![]() cm;③cos∠AOB=
cm;③cos∠AOB= ![]() ;④四边形ABOC是菱形.其中正确结论的序号是( )
;④四边形ABOC是菱形.其中正确结论的序号是( )
A.①③
B.①②③④
C.①②④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在横线上完成下面的证明,并在括号内注明理由.
已知:如图,∠ABC+∠BGD=180°,∠1=∠2.
求证:EF∥DB.
证明:∵∠ABC+∠BGD=180°,(已知)
∴ .( )
∴∠1=∠3.( )
又∵∠1=∠2,(已知)
∴ .( )
∴EF∥DB.( )

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com