
分析 设$\frac{x+y}{2}$=$\frac{y+z}{4}$=$\frac{x+z}{3}$=k,则x+y=2k,y+z=4k,x+z=3k,求出2x+2y+2z=9k,即可求出k,得出方程组,求出方程组的解即可.
解答 解:设$\frac{x+y}{2}$=$\frac{y+z}{4}$=$\frac{x+z}{3}$=k,
则x+y=2k,y+z=4k,x+z=3k,
2x+2y+2z=9k,
∵x+y+z=27,
∴9k=54,
k=6,
即$\left\{\begin{array}{l}{x+y=12}\\{y+z=24}\\{x+z=18}\end{array}\right.$,
解得:x=3,y=8,z=15,
故答案为:3,8,15.
点评 本题考查了解三元一次方程组,能求出k的值是解此题的关键.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
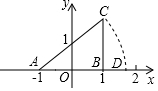 如图,Rt△ABC的边AB在x轴上,且A(-1,0),B(1,0),∠A=45°,斜边AC以点A为旋转中心,顺时针旋转45°,恰好与x轴相交于D,则点D的坐标是( )
如图,Rt△ABC的边AB在x轴上,且A(-1,0),B(1,0),∠A=45°,斜边AC以点A为旋转中心,顺时针旋转45°,恰好与x轴相交于D,则点D的坐标是( )| A. | ($\sqrt{2}$,0) | B. | (2$\sqrt{2}$,0) | C. | (2$\sqrt{2}$-1,0) | D. | (2$\sqrt{2}$-2,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=-$\frac{1}{4}$x2-$\frac{1}{2}$x+$\frac{3}{4}$与x轴交于A,C两点(点A在点C的左边).直线y=kx+b(k≠0)分别交x轴,y轴于A,B两点,且除了点A之外,该直线与抛物线没有其它任何交点.
如图,抛物线y=-$\frac{1}{4}$x2-$\frac{1}{2}$x+$\frac{3}{4}$与x轴交于A,C两点(点A在点C的左边).直线y=kx+b(k≠0)分别交x轴,y轴于A,B两点,且除了点A之外,该直线与抛物线没有其它任何交点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
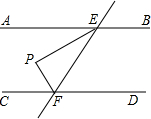 如图,AB∥CD,直线EF与AB,CD分别相交于点E、F,EP平分∠AEF,FP平分∠EFC.
如图,AB∥CD,直线EF与AB,CD分别相交于点E、F,EP平分∠AEF,FP平分∠EFC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com