
����Ŀ����ͼ1��![]() �У�
��![]() ��������
��������![]() ��ͼ1�ڷţ�ʹ���εİ뾶
��ͼ1�ڷţ�ʹ���εİ뾶![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �غϣ�
�غϣ�![]() ��
��
����������
��ͼ2����![]() ������������
������������![]() �Ƶ�
�Ƶ�![]() ��ʱ����תһ�ܣ������߶�
��ʱ����תһ�ܣ������߶�![]() ��
��![]() ������ת��Ϊ
������ת��Ϊ![]() ��
��
���֣�ֱ��д��![]() ��
��![]() ��������ϵ��
��������ϵ��
̽������![]()
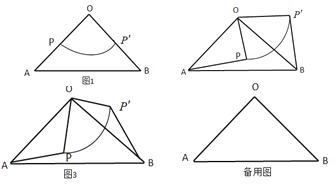
��1������![]() �Ƶ���
�Ƶ���![]() ����࣬��
����࣬��![]() ʱ����ת��
ʱ����ת��![]() ______�㣻
______�㣻
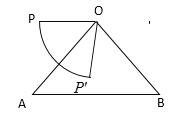
��2������![]() �Ƶ���
�Ƶ���![]() ���Ҳ࣬��
���Ҳ࣬��![]() ��
��![]() ����ʱ����
����ʱ����![]() ��
��
��3������![]() �ǻ�
�ǻ�![]() ������һ�㣬������
������һ�㣬������![]() �Ƶ�
�Ƶ�![]() ��ʱ��ת�����У���
��ʱ��ת�����У���![]() ��������ʱ��ֱ��д��
��������ʱ��ֱ��д��![]() �Ķ�����
�Ķ�����
���죺��ͼ3����![]() ����
����![]() ��
��![]() ��
��![]() ���㹲��ʱ��ֱ��д���߶�
���㹲��ʱ��ֱ��д���߶�![]() �ij���
�ij���
���𰸡�����![]() ��̽������1��310����2��
��̽������1��310����2��![]() ����3��
����3��![]() ��
��![]() �����죺
�����죺![]() ��
��![]() ��
��
��������
���֣�����OA=OB��OP=O![]() ���ɵõ�
���ɵõ�![]() ��
��
̽������1���������⻭��ͼ�Σ���OP��AB�õ���AOP=��A=50�������������ת��![]()
![]() ��
��
��2����![]() ��
��![]() ���еõ�
���еõ�![]() ��ֱ�������Σ����ݹ��ɶ������AP���ɵõ�B
��ֱ�������Σ����ݹ��ɶ������AP���ɵõ�B![]() ��
��
��3������![]() �����=OQ���Թ���A��OQ�ĸ��ߵĻ���һ�룬�ʵ�����ǡ����OAʱ��
�����=OQ���Թ���A��OQ�ĸ��ߵĻ���һ�룬�ʵ�����ǡ����OAʱ��![]() ���������ɴ˵õ�
���������ɴ˵õ�![]() �Ķ�����
�Ķ�����
���죺�������⻭��ͼ�Σ����õ��������ε����ߺ�һ�����ʼ����Ǻ������OH�����ù��ɶ������AH�����ɵõ���.
���֣���OA=OB��OP=O![]() ��
��
��OA-OP=OB-O![]() ��
��
��![]() ��
��
̽����
��1����ͼ��
��![]() ��OA=OB��
��OA=OB��
���A=��B=50����
��OP��AB��
���AOP=��A=50����
����ת��![]()
![]() ��
��
�ʴ�Ϊ��310��
��2���⣺��![]() ��
��![]() ����
����
��![]() ��
��![]() ��ֱ�������Σ�
��ֱ�������Σ�
��![]() ��
��
��![]() ��
��
��3���ߵ�Q��![]() �ϣ�
�ϣ�
��OQ=OP��
![]() �����=OQ���Թ���A��OQ�ĸ��ߵĻ���һ�룬�ʵ�����ǡ����OAʱ��
�����=OQ���Թ���A��OQ�ĸ��ߵĻ���һ�룬�ʵ�����ǡ����OAʱ��![]() ��������
��������
��![]() =90��-80��=10����
=90��-80��=10����![]() =180��-10��=170����
=180��-10��=170����
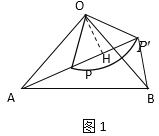
���죺����O��OH��P![]() ��H����ͼ1��
��H����ͼ1��
�ߡ�PO![]() =90����OP=O
=90����OP=O![]() =6��
=6��
��OH=PH=![]() ��
��
��OA=10��
��AH=![]() ,
,
��B![]() =AP=
=AP=![]() ��
��
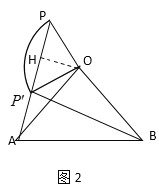
����O��OH��P![]() ��H����ͼ2��
��H����ͼ2��
�ߡ�PO![]() =90����OP=O
=90����OP=O![]() =6��
=6��
��OH=PH=![]() ��
��
��OA=10��
��AH=![]() ,
,
��B![]() =AP=
=AP=![]() ��
��
���߶�![]() �ij�Ϊ
�ij�Ϊ![]() ��
��![]() .
.


 ���ĺ����Ͼ�������ϵ�д�
���ĺ����Ͼ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
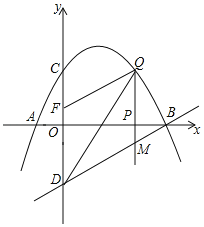
����Ŀ����ͼ����֪������y����![]() +bx+c��ͼ����A(��1��0)�͵�C(0��2)����D���C����x��Գƣ���P��x���ϵ�һ�����㣬���P������Ϊ(m��0)������P��x��Ĵ���l���������ڵ�Q����ֱ��BD�ڵ�M.
+bx+c��ͼ����A(��1��0)�͵�C(0��2)����D���C����x��Գƣ���P��x���ϵ�һ�����㣬���P������Ϊ(m��0)������P��x��Ĵ���l���������ڵ�Q����ֱ��BD�ڵ�M.
(1)�������������ʾ�Ķ��κ����ı���ʽ.
(2)��֪��F(0��![]() )������P��x�����������˶�ʱ������mΪ��ֵʱ���ı���DMQF��ƽ���ı��Σ�
)������P��x�����������˶�ʱ������mΪ��ֵʱ���ı���DMQF��ƽ���ı��Σ�
(3)��P���߶�AB�˶������У��Ƿ���ڵ�Q��ʹ���Ե�B��Q��MΪ��������������BOD���ƣ������ڣ������Q�����ꣻ�������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
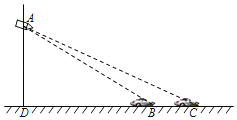
����Ŀ����ͼ��һ���γ��ھ���ij·�ڵĸ�Ӧ��B��C��ʱ�����۵Ƹ��ϵĵ��Ӿ������㵽������Ƭ������Ӧ��֮�����BCΪ6m���ڸ�Ӧ��B��C������õ��Ӿ���A�����Ƿֱ�Ϊ��ABD��18������ACD��14��������Ӿ��찲װ�����۵Ƹ��ϵĸ߶�AD�ij���
���ο����ݣ�sin14���0.242��cos14���0.97��tan14���0.25��sin18���0.309��cos18���0.951��tan18���0.325��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ʦҪ��ÿ��ÿѧ�ڶ�4~7���飬���������˱�ѧ��ѧ�����������������������Ƴɲ�����������ͼ�Ͳ�����������ͼ����������ͼ��ī���ڸ���һ���֣��ش��������⣺
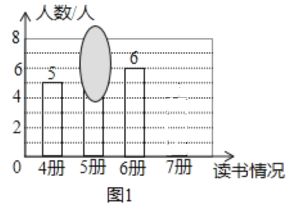

��1�����������ʦ�������˶�����ѧ����
��2����֪��������λ����5��
�μ�˵������ͼ�б��ڸǵ���Ϊ5
��˵������ͼ�б��ڸǵ���Ϊ6
������Ϊ�μκ���˭˵����ȷ����˵��ԭ��������ͼ����������
��������ͼ�У���7�ᡱ�������Ե�Բ�Ľ�Ϊ_______�㣬��������ͼ����������
��3����ֱ��д�����ӳ��ѧ������ȡ���ˣ�ǡ�ö���7����ĸ���Ϊ_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
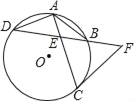
����Ŀ����ͼ��ʾ����O�У���AC��BD����E��![]() ��
��
��1����֤��![]() ��
��
��2���ӳ�EB��F��ʹEF��CF�����ж�CF����O��λ�ù�ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
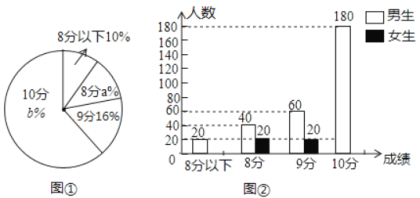
����Ŀ��ij��ѧ�Ա�У2018��500��ѧ�����п���������������е��飬��������1000��Ů��800�ײ��Գɼ����������Ƴɲ�������ͳ��ͼ��ͼ�٣�ͼ�ڣ��������ͳ��ͼ�ṩ����Ϣ������������⣺
��1����У��ҵ���������� �ˣ�����ͳ��ͼ��![]() ��500��ѧ�����п��������Գɼ�����λ���� ��
��500��ѧ�����п��������Գɼ�����λ���� ��
��2����ȫ����ͳ��ͼ��
��3����500��ѧ���������ȡһ��ѧ��������ѧ������ɼ���8�ּ�8�����µĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���O��б��AB�ϣ���OΪԲ�ģ�OBΪ�뾶��Բ���ֱ���BC��AB�ཻ�ڵ�D��E������AD����֪��CAD=��B,
��1����֤��AD�ǡ�O�����ߣ�
��2����BC=8��tanB=![]() �����O �İ뾶��
�����O �İ뾶��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
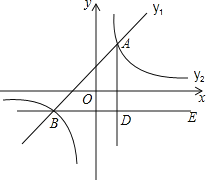
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���![]() ��ͼ���뷴��������
��ͼ���뷴��������![]() ��ͼ���ڵ�
��ͼ���ڵ�![]() ��
��![]() ��
��
![]() ��һ�κ����ͷ����������ı���ʽ��
��һ�κ����ͷ����������ı���ʽ��
![]() ��ֱ��д��
��ֱ��д��![]() ʱ��x��ȡֵ��Χ��
ʱ��x��ȡֵ��Χ��
![]() ����B��
����B��![]() �ᣬ
�ᣬ![]() �ڵ�D����C��ֱ��BE��һ�㣬��
�ڵ�D����C��ֱ��BE��һ�㣬��![]() �����C�����꣮
�����C�����꣮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com