
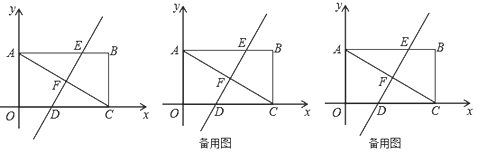
【题目】如图,平面直角坐标系中,矩形![]() 的对角线
的对角线![]() ,
,![]() .
.
(1)把矩形![]() 沿直线
沿直线![]() 对折,使点
对折,使点![]() 落在点
落在点![]() 处,折痕
处,折痕![]() 分别与
分别与![]() 、
、![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() 、
、![]() ,求直线
,求直线![]() 的解析式;
的解析式;
(2)若点![]() 在直线
在直线![]() 上,平面内是否存在点
上,平面内是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,请直接写出点
为顶点的四边形是菱形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在;N点坐标为:
;(2)存在;N点坐标为:![]() ,
,![]() ,
,![]() .
.
【解析】
(1)由含30度直角三角形性质,得OA=![]() AC=12,然后求出OC,然后求得直线AC的解析式,由折叠知DE⊥AC,点F是AC中点,然后可以求得DE的解析式;
AC=12,然后求出OC,然后求得直线AC的解析式,由折叠知DE⊥AC,点F是AC中点,然后可以求得DE的解析式;
(2)分为①以OF,FM为边;②以FM为边,OF为对角线;③以OF为边,FM为对角线,三类进行讨论分析,然后可求N点坐标.
解:(1)根据题意,在直角三角形AOC中,∠AOC=90°,![]() ,
,![]() ,
,
∴![]() ,即点A为:(0,12),
,即点A为:(0,12),
由勾股定理,得![]() ,即点C为:(
,即点C为:(![]() ),
),
设直线AC的方程为![]() ,把A、C坐标代入,得
,把A、C坐标代入,得
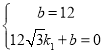 ,解得:
,解得: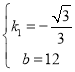 ,
,
∴直线AC的方程为:![]() ,
,
根据折叠的性质,有DE⊥AC,点F是AC中点,
∴直线DE的斜率为:![]() ,点F为(
,点F为(![]() ),
),
则设直线DE的解析式为![]() ,把点F代入,得
,把点F代入,得
![]() ,解得:
,解得:![]() ,
,
∴直线DE的解析式为:![]() ;
;
(2)存在;
①以OF,FM为边,如图
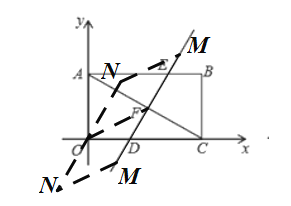
由(1)知,直线DE的解析式为:![]() ,
,
令![]() ,则
,则![]() ,
,
∴点D坐标为:![]() ,
,
∵ONMF是菱形
∴OF=ON,ON∥DE
∴直线ON的解析式为:![]() ,
,
设N点坐标为:(![]() ),
),
∴![]() ,
,![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴N点坐标为:![]() ;
;
②以FM为边,OF为对角线;连接AD,CE,如图:
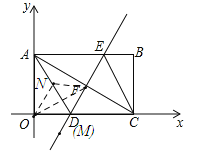
由折叠知,四边形ADCE是菱形,
∴AD=CD=![]() ,
,
∴∠DAC=∠DCA=30°,
∴∠OAD=30°,
∴∠OAD=∠DAC,AD=AD,∠AOD=∠AFD=90°,
∴△AOD≌△AFD,
∴AO=AF,OD=FD,
∴AD是OF 的垂直平分线,
∵四边形ONFM是菱形,
∴MN是OF的垂直平分线,
∴M与D重合,即M为![]() ,
,
设N为![]() ,
,
∵OF与MN互相平分,
∴![]() ,
,![]() ,
,
解得:![]() ,
,
∴N点坐标为:![]() ;
;
③以OF为边,FM为对角线,如图:
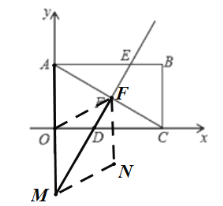
∵直线DE的解析式为:![]() ,
,
∴直线DE与y轴的交点为(0,-12),
∵四边形OFNM是菱形,![]() ,
,
∴OM=OF=12,
∴点M的坐标为(0,-12),
∵OM∥FN,OM=FN=12,且点F为(![]() ),
),
∴N点坐标为:![]() ;
;
综合上述,N点坐标为:![]() ,
,![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
【题目】甲骑自行车从M地出发沿一条公路匀速前往N地,乙骑摩托车从N地出发沿同一条公路匀速前往M地,
已知乙比甲晚出发0.5小时且先到达目的地.设甲行驶的时间为t(h),甲乙两人之间的路程为y(km),
y与t的函数关系如图1所示,请解决以下问题:
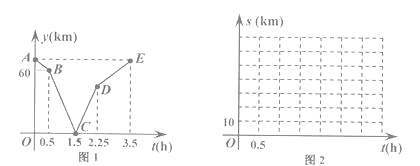
(1)写出图1中点C表示的实际意义并求线段BC所在直线的函数表达式.
(2)①求点D的纵坐标.
②求M,N两地之间的距离.
(3)设乙离M地的路程为S乙 (km),请直接写出S甲 与时间t(h)的函数表达式,并在图2所给的直角坐标系中画出它的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠MAN=120°,AC平分∠MAN,点B、D分别在AN、AM上.
(1)如图1,若∠ABC=∠ADC=90°,请你探索线段AD、AB、AC之间的数量关系,并证明之;
(2)如图2,若∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.
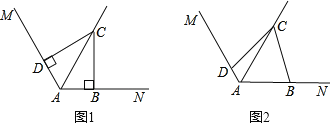
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
(实践操作)三角尺中的数学
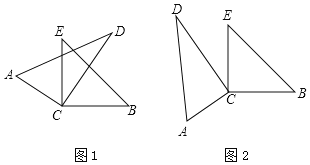
数学实践活动课上,“奋进”小组将一副直角三角尺的直角顶点叠放在一起,如图1,使直角顶点重合于点C.
(问题发现)
(1)①填空:如图1,若∠ACB=145°,则∠ACE的度数是 ,∠DCB的度数 ,∠ECD的度数是 .
②如图1,你发现∠ACE与∠DCB的大小有何关系?∠ACB与∠ECD的大小又有何关系?请直接写出你发现的结论.
(类比探究)
(2)如图2,当△ACD与△BCE没有重合部分时,上述②中你发现的结论是否还依然成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
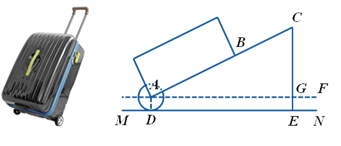
【题目】有一只拉杆式旅行箱(图1),其侧面示意图如图2所示.已知箱体长AB=50cm,拉杆![]() 的伸长距离最大时可达35cm,点A,B,C在同一条直线上.在箱体底端装有圆形的滚轮⊙A,⊙A与水平地面MN相切于点D.在拉杆伸长至最大的情况下,当点B距离水平地面38cm时,点C到水平地面的距离CE为59cm.
的伸长距离最大时可达35cm,点A,B,C在同一条直线上.在箱体底端装有圆形的滚轮⊙A,⊙A与水平地面MN相切于点D.在拉杆伸长至最大的情况下,当点B距离水平地面38cm时,点C到水平地面的距离CE为59cm.
设AF∥MN.
(1)求⊙A的半径长;
(2)当人的手自然下垂拉旅行箱时,人感到较为舒服.某人将手自然下垂在C端拉旅行箱时,CE为80cm,![]() =64°.求此时拉杆BC的伸长距离.(精确到1cm,参考数据:
=64°.求此时拉杆BC的伸长距离.(精确到1cm,参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,点P的坐标为(m,n),则向量![]() 可以用点P的坐标表示为
可以用点P的坐标表示为![]() =(m,n);已知
=(m,n);已知![]() =(x1,y1),
=(x1,y1),![]() =(x2,y2),若x1x2+y1y2=0,则
=(x2,y2),若x1x2+y1y2=0,则![]() 与
与![]() 互相垂直.
互相垂直.
下面四组向量:①![]() =(3,﹣9),
=(3,﹣9),![]() =(1,﹣
=(1,﹣![]() );
);
②![]() =(2,π0),
=(2,π0),![]() =(2﹣1,﹣1);
=(2﹣1,﹣1);
③![]() =(cos30°,tan45°),
=(cos30°,tan45°),![]() =(sin30°,tan45°);
=(sin30°,tan45°);
④![]() =(
=(![]() +2,
+2,![]() ),
),![]() =(
=(![]() ﹣2,
﹣2,![]() ).
).
其中互相垂直的组有( )
A. 1组 B. 2组 C. 3组 D. 4组
查看答案和解析>>
科目:初中数学 来源: 题型:
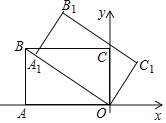
【题目】如图,平面直角坐标系中,矩形OABC的顶点A(﹣6,0),C(0,2![]() ).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.
).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, BD 是△ABC 的角平分线, AE⊥ BD ,垂足为 F ,若∠ABC=35°,∠ C=50°,则∠CDE 的度数为( )

A.35°B.40°C.45°D.50°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com