
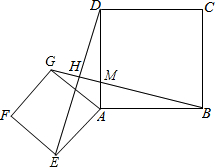
 如图,点E是正方形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个正方形AEFG,线段GB与线段ED,AD分别交于点H,M.
如图,点E是正方形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个正方形AEFG,线段GB与线段ED,AD分别交于点H,M.| 2 |
| 2 |
| 2 |
| 2 |
|
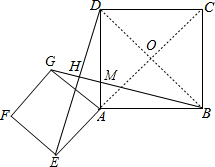 (3)解:连接BD和AC,两线交于O,
(3)解:连接BD和AC,两线交于O,| 22+22 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| DO2+EO2 |
| 10 |
| 10 |


科目:初中数学 来源: 题型:
| A、了解湖州电视台“阿奇讲事体”栏目的收视率 |
| B、了解某甲型H1N1确诊病人同机乘客的健康状况 |
| C、了解某班每个学生家庭电脑的数量 |
| D、“神十”载人飞船发射前对重要零部件的检查 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n(n+1) |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2002×2003 |
查看答案和解析>>
科目:初中数学 来源: 题型:
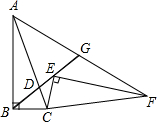 如图,在Rt△ABC中,∠B=90°,sin∠BAC=
如图,在Rt△ABC中,∠B=90°,sin∠BAC=| 1 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com