

 cm/s,即可求得答案.
cm/s,即可求得答案. 解:(1)连接OQ,
解:(1)连接OQ, (cm)(4分)
(cm)(4分) (6分)
(6分) -2
-2 t=10
t=10
 ,
, t-10
t-10 =10,
=10,
 ,
,
 时,直线AB与⊙O相切.(8分)
时,直线AB与⊙O相切.(8分) cm/s,
cm/s, =5-
=5- ,t2=
,t2= =5+
=5+
 秒时,相交的弦长是16cm.(12分)
秒时,相交的弦长是16cm.(12分)

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 结果保留根号)
结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| 2 |
 为(x,y),问N点的坐标x,y能否写成与r无关的关系式?若能,请写出关系式;若不能,请说明理由.
为(x,y),问N点的坐标x,y能否写成与r无关的关系式?若能,请写出关系式;若不能,请说明理由.查看答案和解析>>
科目:初中数学 来源:2013-2014学年广东汕头友联中学九年级上学期第二次阶段测试数学试卷(解析版) 题型:解答题
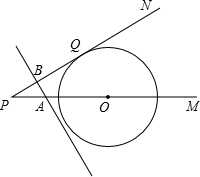
如图,已知⊙O的圆心O在射线PM上,PN切⊙O于Q,PO=20cm,∠P=30°,A、B两点同时从P点出发,点A沿PN方向移动,点B以4cm/s的速度沿PM方向移动,且直线AB始终垂直PN.设运动时间为t秒,求下列问题.(结果保留根号)

(1)求PQ的长
(2)当t为何值时直线AB与⊙o相切?
查看答案和解析>>
科目:初中数学 来源:2002年湖北省黄石市中考数学试卷(解析版) 题型:解答题
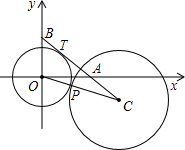
 ,
, )的切线交x轴于A点,交y轴于B点.
)的切线交x轴于A点,交y轴于B点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com