
分析 (1)先算二次根式,三次根式,再相加减即可求解;
(2)先算二次根式,再相加减即可求解;
(3)先算二次根式,三次根式,再算除法,再相加减即可求解;
(4)(5)利用平方差公式分母有理化即可求解;
(6)利用平方差公式分母有理化,再合并同类项即可求解.
解答 解:(1)$\sqrt{0.01}$+$\root{3}{-27}$-$\sqrt{\frac{1}{100}}$
=0.1-3-0.1
=-3;
(2)$\sqrt{24}$-$\sqrt{0.5}$+2$\sqrt{\frac{2}{3}}$+3$\sqrt{8}$
=2$\sqrt{6}$-$\frac{\sqrt{2}}{2}$+$\frac{2}{3}$$\sqrt{6}$+6$\sqrt{2}$
=$\frac{8}{3}$$\sqrt{6}$+$\frac{11}{2}$$\sqrt{2}$;
(3)$\sqrt{\frac{2}{3}}$-4×$\root{3}{216}$+42$\sqrt{\frac{1}{6}}$
=$\frac{\sqrt{6}}{3}$-4×6+7$\sqrt{6}$
=$\frac{22}{3}$$\sqrt{6}$-24;
(4)$\frac{2}{{2+\sqrt{3}}}$=$\frac{2(2-\sqrt{3})}{(2+\sqrt{3})(2-\sqrt{3})}$=4-2$\sqrt{3}$;
(5)$\frac{4}{{\sqrt{3}-\sqrt{5}}}$=$\frac{4(\sqrt{3}+\sqrt{5})}{(\sqrt{3}-\sqrt{5})(\sqrt{3}+\sqrt{5})}$=-2$\sqrt{3}$-2$\sqrt{5}$;
(6)$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{2}+1}$-$\frac{2}{\sqrt{3}+1}$
=$\sqrt{3}$-$\sqrt{2}$+$\sqrt{2}$-1-$\sqrt{3}$+1
=0.
点评 考查了实数的运算,关键是熟练掌握二次根式,三次根式,平方差公式,分母有理化,合并同类项的计算法则.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:解答题
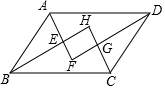 如图,在?ABCD中,AF、BH、CH、DF分别是∠DAB、∠ABC、∠BCD、∠CDA的平分线,AF与BH交于点E,CH与DF交于点G.在不添加其他条件的情况下,试写出上述条件推出的结论,并选择你喜欢的一个结论说明成立的理由.(要求推理过程中用到″平行四边形″和″角平分线″这两个条件).
如图,在?ABCD中,AF、BH、CH、DF分别是∠DAB、∠ABC、∠BCD、∠CDA的平分线,AF与BH交于点E,CH与DF交于点G.在不添加其他条件的情况下,试写出上述条件推出的结论,并选择你喜欢的一个结论说明成立的理由.(要求推理过程中用到″平行四边形″和″角平分线″这两个条件).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
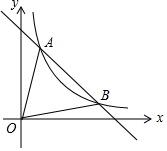 如图,由正比例函数y=-x沿y轴的正方向平移4个单位而成的一次函数y=-x+b的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B两点.
如图,由正比例函数y=-x沿y轴的正方向平移4个单位而成的一次函数y=-x+b的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ③ | D. | ①③ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
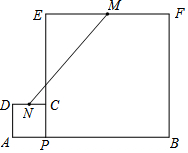 如图,线段AB=10,点P在线段AB上,在AB的同侧分别以AP、BP为边长作正方形APCD和BPEF,点M、N分别是EF、CD的中点,则MN的最小值是5.
如图,线段AB=10,点P在线段AB上,在AB的同侧分别以AP、BP为边长作正方形APCD和BPEF,点M、N分别是EF、CD的中点,则MN的最小值是5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com