
【题目】如图,OB为∠AOC内一条射线,∠AOB的余角是它自身的两倍.
(1)求∠AOB的度数;
(2)射线OE从OA开始,在∠AOB内以1°/s的速度绕着O点逆时针方向旋转,转到OB停止,同时射线OF在∠BOC内从OB开始以3°/s的速度绕O点逆时针方向旋转转到OC停止,设运动时间为t秒.
①若OE,OF运动的任一时刻,均有∠COF=3∠BOE,求∠AOC的度数;
②OP为∠AOC内任一射线,在①的条件下,当t=10时,以OP为边所有角的度数和的最小值为 .

【答案】(1)30°;(2)①120°,②170°.
【解析】
(1)根据余角的定义列方程解答即可;
(2)①分别用t的代数式表示出∠AOE、∠BOF,∠BOE,根据∠COF=3∠BOE列方程解答即可;
②当OP与OB重合时,以OP为边所有角的度数和的有最小值,把t=10代入计算即可.
解:(1)设∠AOB=x![]() ,则∠AOB的余角=(90﹣x)
,则∠AOB的余角=(90﹣x)![]() ,
,
依题意有:∴90﹣x=2x,
∴x=30,
∴∠AOB=30°;
(2)①∵运动时间为t秒,则
∠AOE=t°,∠BOF=3t°,∠BOE=(30﹣t)°,
∠COF=∠AOC﹣∠AOB﹣∠BOF,
设∠AOC=y°,
又∵∠COF=3∠BOE,
则有:y﹣30﹣3t=3(30﹣t),
解得:y=120,
∴∠AOC=120°,
②当OP与OB重合时,以OP为边所有角的度数和的有最小值,
当t=10时,以OP为边所有角的度数和的最小值为170°.
故答案为:170°



科目:初中数学 来源: 题型:
【题目】学生参加植树造林,甲班每天比乙班多植5棵树,甲班植80棵树与乙班植70棵树所用的天数相等,求甲、乙两班每天各植树多少棵。下面列式错误的是 ( )
A.设甲班每天植树x棵,则![]() B.设乙班每天植树x棵,则
B.设乙班每天植树x棵,则![]()
C.设甲班在x天植树80棵,则![]() D.设乙班在x天植树70棵,则
D.设乙班在x天植树70棵,则![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
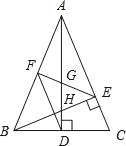
【题目】如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE,BE分别交于点G、H.有下列结论:①FD=FE;②AH=2CD;③BCAD=![]() AE2;④S△ABC=2S△ADF.其中正确结论的序号是_____.(把你认为正确结论的序号都填上)
AE2;④S△ABC=2S△ADF.其中正确结论的序号是_____.(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某食品厂从生产的袋装食品中抽出样品20袋,以每袋标准质量45克为标准,检测每袋的质量是否符合该标准,超过或不足的克数分别用正、负数来表示,记录如下:
与标准质量的差值(单位:克) | ﹣5 | ﹣3 | 0 | 1 | 2 | 5 |
袋数 | 1 | 3 | 6 | 4 | 5 | 1 |
回答下列问题:
(1)这20袋样品中,完全符合每袋标准质量45克的有 袋;
(2)这批样品的总质量是多少克?(要求写出算式).
查看答案和解析>>
科目:初中数学 来源: 题型:
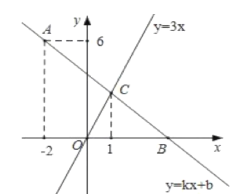
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求一次函数y=kx+b的解析式;
(2)若点D在y轴负半轴上,且满足S△COD═![]() S△BOC,请直接写出点D的坐标.
S△BOC,请直接写出点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实党的“精准扶贫”政策,A.,B两城决定向C,D两乡运送肥料以支持农村生产,已知A,B两城共有肥料500吨,其中A城肥料比B城少100吨,从A城往C,D两乡运肥料的费用分别为20元/吨和25元/吨;从B城往C, D两乡运肥料的费用分别为15元/吨和24元/吨。现C乡需要肥料240吨,D乡需要肥料260吨.
(1)A城和B城各有多少吨肥料?
(2)设从A城运往C乡肥料x吨,总运费为y元,求出最少总运费.
(3)由于更换车型,使A城运往C乡的运费每吨减少a(0<a<6)元,这时怎样调运才能使总运费最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
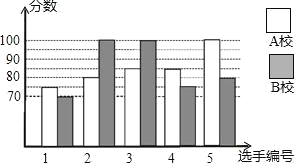
【题目】某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
(1)根据图示填写下表:
平均数/分 | 中位数/分 | 众数/分 | |
A校 | ______ | 85 | ______ |
B校 | 85 | ______ | 100 |
(2)结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
(3)计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
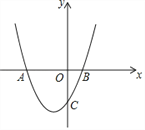
【题目】已知:二次函数y=ax2+2ax﹣4(a≠0)的图象与x轴交于点A,B(A点在B点的左侧),与y轴交于点C,△ABC的面积为12.
(1)求二次函数图象的对称轴与它的解析式;
(2)点D在y轴上,当以A、O、D为顶点的三角形与△BOC相似时,求点D的坐标;
(3)点D的坐标为(﹣2,1),点P在二次函数图象上,∠ADP为锐角,且tan∠ADP=2,求点P的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴的原点为O,点A、B、C是数轴上的三点,点B对应的数为1,AB=8,BC=3,动点P、Q同时从A、C出发,分别以每秒2个长度单位和每秒1个长度单位的速度沿数轴正方向运动.设运动时间为t秒(t>0)
(1)求点A、C分别对应的数;
(2)求点P、Q分别对应的数;(用含t的式子表示)
(3)试问当t为何值时,OP=OQ?
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com