
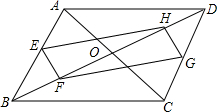
 如图所示,在?ABCD中,AC,BD交于点O,其中E、F、G、H分别是AB,OB,CD,OD的中点.求证:∠HEF=∠FGH.
如图所示,在?ABCD中,AC,BD交于点O,其中E、F、G、H分别是AB,OB,CD,OD的中点.求证:∠HEF=∠FGH. 分析 先证EF、GH分别是△ABO、△CDO的中位线,证出EF∥GH,EF=GH,再证明四边形EFGH时平行四边形,根据平行四边形的对角相等即可得出结论.
解答 证明:∵四边形ABCD是平行四边形,
∴OA=OC,
∵E、F、G、H分别是AB,OB,CD,OD的中点,
∴EF、GH分别是△ABO、△CDO的中位线,
∴EF∥OA,EF=$\frac{1}{2}$OA,GH∥OC,GH=$\frac{1}{2}$OC,
∴EF∥GH,EF=GH,
∴四边形EFGH时平行四边形,
∴∠HEF=∠FGH.
点评 本题考查了平行四边形的判定与性质以及三角形中位线定理;根据三角形中位线定理证出四边形是平行四边形是解决问题的关键.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校为了解2014年八年级学生课外书籍借阅情况,从中随机抽取了50名学生课外书籍借阅情况,将统计结果列出如下的表格,并绘制成如图所示的扇形统计图,其中科普类册数占这50名学生借阅总册数的40%.
某校为了解2014年八年级学生课外书籍借阅情况,从中随机抽取了50名学生课外书籍借阅情况,将统计结果列出如下的表格,并绘制成如图所示的扇形统计图,其中科普类册数占这50名学生借阅总册数的40%.| 类别 | 科普类 | 教辅类 | 文艺类 | 其他 |
| 册数(本) | 168 | 105 | m | 32 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动;同时动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动.若以A、M、N为顶点的三角形与△ACD相似,则运动的时间t为2.4或1.5秒.
如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动;同时动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动.若以A、M、N为顶点的三角形与△ACD相似,则运动的时间t为2.4或1.5秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com