

| OF2+BE2 | 2EF2 |
| 4 |
| a |
| OF2+BE2 |
| 2EF2 |
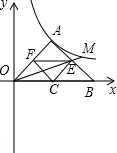
 НтЃКЃЈ1ЃЉЙ§ЕуAзїAEЁЭOBгкEЃЎ
НтЃКЃЈ1ЃЉЙ§ЕуAзїAEЁЭOBгкEЃЎ| 1 |
| 2 |
| k |
| x |
| k |
| 2 |
| 4 |
| x |
|
|
| 4 |
| a |
| 4|a| |
| 2 |
| OF2+BE2 |
| 2EF2 |
| 1 |
| 2 |
| OF2+BE2 |
| 2EF2 |
| 1 |
| 2 |


 вЛХЕЪщвЕЪюМйзївЕПьРжМйЦкдЦФЯУРЪѕГіАцЩчЯЕСаД№АИ
вЛХЕЪщвЕЪюМйзївЕПьРжМйЦкдЦФЯУРЪѕГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
 8ЁЂШчЭМЃЌЙ§ЕуPЛГіЩфЯпPMЃЌPNЃЌЪЙPMЁЮOAЃЌPNЁЮOBЃЌЧвЩфЯпPMКЭЩфЯпOAЃЌЩфЯпPNКЭЩфЯпOBЗНЯђЗжБ№ЯрЭЌЃЌСПвЛСПЁЯOКЭЁЯPЃЌФуФмЕУЕНЪВУДНсТлЃПШчЙћЩфЯпPMКЭЩфЯпOAЃЌЩфЯпPNКЭЩфЯпOBвЛзщЗНЯђЯрЭЌЁЂСэвЛзщЗНЯђЯрЗДЃЌЁЯOКЭЁЯPгжгаЪВУДЙиЯЕФиЃПШчЙћСНзщЗНЯђЖМЯрЗДЃЌЁЯOКЭЁЯPгаЪВУДЙиЯЕЃП
8ЁЂШчЭМЃЌЙ§ЕуPЛГіЩфЯпPMЃЌPNЃЌЪЙPMЁЮOAЃЌPNЁЮOBЃЌЧвЩфЯпPMКЭЩфЯпOAЃЌЩфЯпPNКЭЩфЯпOBЗНЯђЗжБ№ЯрЭЌЃЌСПвЛСПЁЯOКЭЁЯPЃЌФуФмЕУЕНЪВУДНсТлЃПШчЙћЩфЯпPMКЭЩфЯпOAЃЌЩфЯпPNКЭЩфЯпOBвЛзщЗНЯђЯрЭЌЁЂСэвЛзщЗНЯђЯрЗДЃЌЁЯOКЭЁЯPгжгаЪВУДЙиЯЕФиЃПШчЙћСНзщЗНЯђЖМЯрЗДЃЌЁЯOКЭЁЯPгаЪВУДЙиЯЕЃПВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
| ||||
| a+2 |
| k |
| 2 |
| k |
| 2 |
| PM+PN |
| NM |
| PM-PN |
| AM |

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
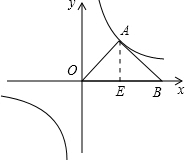
 ШчЭМЃЌЙ§ЕуOЁЂAЃЈ1ЃЌ0ЃЉЁЂBЃЈ0ЃЌ
ШчЭМЃЌЙ§ЕуOЁЂAЃЈ1ЃЌ0ЃЉЁЂBЃЈ0ЃЌ| 3 |
| AЁЂ60Ёу |
| BЁЂ60ЁуЛђ120Ёу |
| CЁЂ30Ёу |
| DЁЂ30ЁуЛђ150Ёу |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
 ШчЭМЃЌЙ§ЕуPЃЈ2ЃЌ
ШчЭМЃЌЙ§ЕуPЃЈ2ЃЌ| 2 |
| k |
| x |
| k |
| x |
| k |
| x |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
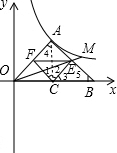
 ШчЭМЃЌЙ§ЕуAЃЈ1ЃЌ0ЃЉЕФжБЯпгыyжсЦНааЃЌЧвЗжБ№гые§БШР§КЏЪ§y=k1xЃЌy=k2xКЭЗДБШР§y=
ШчЭМЃЌЙ§ЕуAЃЈ1ЃЌ0ЃЉЕФжБЯпгыyжсЦНааЃЌЧвЗжБ№гые§БШР§КЏЪ§y=k1xЃЌy=k2xКЭЗДБШР§y=| k3 | x |
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com