
【题目】已知抛物线y=3ax2+2bx+c.
(1)若a=b=1,c=﹣1,求抛物线与x轴公共点的坐标;
(2)若a=b=1,且当﹣1<x<1时,抛物线与x轴有且只有一个公共点,求c的取值范围.
【答案】
(1)解:∵a=b=1,c=﹣1,
∴抛物线的解析式为y=3x2+2x﹣1,
令y=3x2+2x﹣1=0,解得:x=﹣1或 ![]() ,
,
∴抛物线与x轴的交点坐标为:(﹣1,0),( ![]() ,0)
,0)
(2)解:∵a=b=1,
∴解析式为y=3x2+2x+c.
∵对称轴x=﹣ ![]() =﹣
=﹣ ![]() ,
,
∴当﹣1<x<1时,抛物线与x轴有且只有一个公共点,
则①此公共点一定是顶点,
∴△=4﹣12c=0,
②一个交点的横坐标小于等于﹣1,另一交点的横坐标小于1而大于﹣1,
∴3﹣2+c≤0,3+2+c>0,
解得﹣5<c≤﹣1.
综上所述,c的取值范围是:c= ![]() 或﹣5<c≤﹣1
或﹣5<c≤﹣1
【解析】(1)将a、b、c的值代入抛物线后求得解析式,令y=0求出x的值就是交点坐标的横坐标;(2)根据其在此范围内有一个交点,此时将两个值代入,分别大于零和小于零,进而求出相应的取值范围.
【考点精析】认真审题,首先需要了解抛物线与坐标轴的交点(一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.).


科目:初中数学 来源: 题型:
【题目】在下列条件中:①∠A +∠B=∠C;②∠A:∠B:∠C=l:2:3;③∠A=90°-∠B;④∠A=∠B=![]() ∠C中,能确定△ABC是直角三角形的条件有( )
∠C中,能确定△ABC是直角三角形的条件有( )
A. 1个; B. 2个; C. 3个; D. 4个;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“双十二”期间,A,B两个超市开展促销活动,活动方式如下:
A超市:购物金额打9折后,若超过2000元再优惠300元;
B超市:购物金额打8折.
某学校计划购买某品牌的篮球做奖品,该品牌的篮球在A,B两个超市的标价相同.根据商场的活动方式:
(1)若一次性付款4200元购买这种篮球,则在B商场购买的数量比在A商场购买的数量多5个.请求出这种篮球的标价;
(2)学校计划购买100个篮球,请你设计一个购买方案,使所需的费用最少.(直接写出方案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形MNPQ中,动点R从点N出发,沿着N→P→Q→M方向运动至点M处停下,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则下列说法不正确的是( )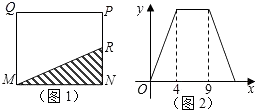
A.当x=2时,y=5
B.矩形MNPQ的面积是20
C.当x=6时,y=10
D.当y= ![]() 时,x=3
时,x=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把△ABC纸片沿DE折叠,当点A在四边形BCDE的外部时,记∠AEB为∠1,∠ADC为∠2,则∠A、∠1与∠2的数量关系,结论正确的是( )

A. ∠1=∠2+∠A B. ∠1=2∠A+∠2
C. ∠1=2∠2+2∠A D. 2∠1=∠2+∠A
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面直角坐标系中,直线y=kx+b与x轴交于点A(6,0),与y轴交于点B,与直线y=2x交于点C(a,4).
(1)求点C的坐标及直线AB的表达式;
(2)如图2,在(1)的条件下,过点E作直线l⊥x轴于点E,交直线y=2x于点F,交直线y=kx+b于点G,若点E的坐标是(4,0).
①求△CGF的面积;
②直线l上是否存在点P,使OP+BP的值最小?若存在,直接写出点P的坐标;若不存在,说明理由;
(3)若(2)中的点E是x轴上的一个动点,点E的横坐标为m(m>0),当点E在x轴上运动时,探究下列问题:
当m取何值时,直线l上存在点Q,使得以A,C,Q为顶点的三角形与△AOC全等?请直接写出相应的m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com