
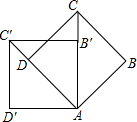
 如图,正方形ABCD旋转后得到正方形AB′C′D′,①旋转角是45度;②若AB=1,则C′D=$\sqrt{2}$-1.
如图,正方形ABCD旋转后得到正方形AB′C′D′,①旋转角是45度;②若AB=1,则C′D=$\sqrt{2}$-1. 分析 ①根据正方形的性质即可得到结论;
②正方形ABCD旋转后得到正方形AB′C′D′,于是得到AD′=C′D′=AB=AD=1,∠D′=90°,根据勾股定理可得答案.
解答 解:①∵ 四边形ABCD,AB′C′D′是正方形,
四边形ABCD,AB′C′D′是正方形,
∴∠D′AD=∠D′AC′=45°,
∴旋转角是45°;
②∵正方形ABCD旋转后得到正方形AB′C′D′,
∴AD′=C′D′=AB=AD=1,∠D′=90°,
∴AC′=$\sqrt{2}$AD′=$\sqrt{2}$,
∴C′D=AC′-AD=$\sqrt{2}$-1,
故答案为:45°,$\sqrt{2}$-1.
点评 本题考查了旋转的性质,正方形的性质,熟练掌握各性质定理是解题的关键.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:选择题
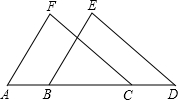 如图所示,△ACF与△BDE全等,点A,B,C,D在同一条直线上,且点F和点E是对应点,点A和点B是对应点,下列结论中,错误的是( )
如图所示,△ACF与△BDE全等,点A,B,C,D在同一条直线上,且点F和点E是对应点,点A和点B是对应点,下列结论中,错误的是( )| A. | AF∥BE | B. | CF∥DE | C. | AB=CD | D. | ∠ACF=∠EBD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.5×10-6 | B. | 0.25×10-6 | C. | 2.5×10-5 | D. | 0.25×10-5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com