
【题目】某公司经销的一种产品每件成本为40元,要求在90天内完成销售任务.已知该产品90天内每天的销售价格与时间(第x天)的关系如下表:
时间(第x天) | 1≤x<50 | 50≤x≤90 |
x+50 | 90 |
任务完成后,统计发现销售员小王90天内日销售量p(件)与时间(第x天)满足一次函数关系p=﹣2x+200.设小王第x天销售利润为W元.
(1)直接写出W与x之间的函数关系式,井注明自变量x的取值范围;
(2)求小生第几天的销售量最大?最大利润是多少?
(3)任务完成后,统计发现平均每个销售员每天销售利润为4800公司制定如下奖励制度:如果一个销售员某天的销售利润超过该平均值,则该销售员当天可获得200元奖金.请计算小王一共可获得多少元奖金?
【答案】(1)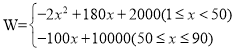 ;(2)小王第45天的销售利润最大,最大利润为6050元;(3)小王一共可获得6200元奖金.
;(2)小王第45天的销售利润最大,最大利润为6050元;(3)小王一共可获得6200元奖金.
【解析】
(1)依据题意销售利润=销售量×(售价-进价)易得出销售利润为W(元)与x(天)之间的函数关系式;
(2)依据(1)中函数的增减性求得最大利润;
(3)根据销售利润为W(元)与x(天)之间的函数关系式,求出利润超过4800元的天数即可求得可获得的奖金金额.
(1)依题意:![]() ,
,
整理得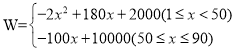 ;
;
(2)①当1≤x<50时,W=﹣2x2+180x+2000=﹣2(x﹣45)2+6050,
∵﹣2<0,
∴抛物线开口向下,
∴当x=45时,W有最大值为6050;
②当50≤x≤90时,W=﹣100x+10000,
∵﹣100<0,
∴W随x的增大而减小,
∴当x=50时,W有最大值为5000,
∵6050>5000,
∴当x=45时,W的值最大,最大值为6050,
即小王第45天的销售利润最大,最大利润为6050元;
(3)①当1≤x<50时,令W=4800,得W=﹣2(x﹣45)2+6050=4800,
解得x1=20,x2=70,
∴当W>4800时,20<x<70,
∵1≤x<50,
∴20<x<50;
②当50≤x≤90时,令W>4800,W=﹣100x+10000>4800,
解得x<52,
∵50≤x≤90,
∴50≤x<52,
综上所述:当20<x<50时,W>4800,即共有51﹣21+1=31天的销售利润超过4800元,
∴可获得奖金200×31=6200元,
即小王一共可获得6200元奖金.


 作业辅导系列答案
作业辅导系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的个数是( )
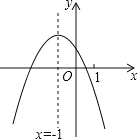
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了估计某地区供暖期间空气质量情况,某同学在20天里做了如下记录:
污染指数(ω) | 40 | 60 | 80 | 100 | 120 | 140 |
天数(天) | 3 | 2 | 3 | 4 | 5 | 3 |
其中ω<50时空气质量为优,50≤ω≤100时空气质量为良,100<ω≤150时空气质量为轻度污染.若按供暖期125天计算,请你估计该地区在供暖期间空气质量达到良以上(含良)的天数为( )
A.75B.65C.85D.100
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是正方形
是正方形![]() 外一点,连接
外一点,连接![]() 交
交 ![]() 于点
于点![]() ,若
,若![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③ 四边形
;③ 四边形![]() 的面积是
的面积是![]() ;④点
;④点![]() 到 直线
到 直线![]() 的距离为
的距离为![]() ;⑤
;⑤![]() .其中结论正确的个数是( )
.其中结论正确的个数是( )
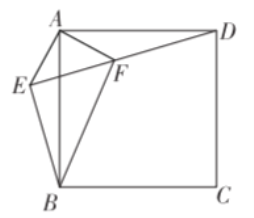
A.![]() B.2C.3D.4
B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在国家政策的宏观调控下,某市的商品房成交均价由今年3月份的14 000元/m2下降到5月份的12 600元/m2.
(1)问4,5两月平均每月降价的百分率约是多少?(参考数据:![]() ≈0.95)
≈0.95)
(2)如果房价继续跌落,按此降价的百分率,你预测到7月份该市的商品房成交均价是否会跌跛10 000元/m2?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个口袋中装有六个完全相同的小球,小球上分别标有1,2,5,7,8,13六个数,搅匀后一次从中摸出一个小球,将小球上的数记为m,则使得一次函数y=(﹣m+1)x+11﹣m经过一、二、四象限且关于x的分式方程![]() =3x+
=3x+![]() 的解为整数的概率是( )
的解为整数的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
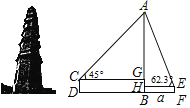
【题目】慈氏塔位于岳阳市城西洞庭湖边,是湖南省保存最好的古塔建筑之一.如图,小亮的目高CD为1.7米,他站在D处测得塔顶的仰角∠ACG为45°,小琴的目高EF为1.5米,她站在距离塔底中心B点a米远的F处,测得塔顶的仰角∠AEH为62.3°.(点D、B、F在同一水平线上,参考数据:sin62.3°≈0.89,cos62.3°≈0.46,tan62.3°≈1.9)
(1)求小亮与塔底中心的距离BD;(用含a的式子表示)
(2)若小亮与小琴相距52米,求慈氏塔的高度AB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com