
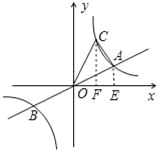
【题目】如图,已知直线![]() 与双曲线y=
与双曲线y=![]() 交于A、B两点,点B的坐标为(-4,-2),C为第一象限内双曲线y=
交于A、B两点,点B的坐标为(-4,-2),C为第一象限内双曲线y=![]() 上一点,且点C在直线
上一点,且点C在直线![]() 的上方.
的上方.

(1)求双曲线的函数解析式;
(2)若△AOC的面积为6,求点C的坐标.
【答案】(1) ![]() ;(2)(2,4)
;(2)(2,4)
【解析】试题分析:(1)利用待定系数法即可解决.
(2)过点A作AE⊥x轴于E,过点C作CF⊥x轴于F,根据![]() =6,列出方程即可解决.
=6,列出方程即可解决.
试题解析:(1)∵点B(﹣4,﹣2)在双曲线y=![]() 上,
上,
∴![]() =﹣2,
=﹣2,
∴k=8,
∴双曲线的函数解析式为y=![]() .
.
(2)过点A作AE⊥x轴于E,过点C作CF⊥x轴于F,
∵正比例函数与反比例函数的交点A、B关于原点对称,
∴A(4,2),∴OE=4,AE=2,
设点C的坐标为(a, ![]() ),则OF=a,CF=
),则OF=a,CF=![]() ,
,
则![]() ,
,
=![]() ×
×![]() +
+![]() (2+
(2+![]() )(4﹣a)﹣
)(4﹣a)﹣![]() ×4×2
×4×2
=![]() ,
,
∵△AOC的面积为6,
∴![]() =6,
=6,
整理得a2+6a﹣16=0,
解得a=2或﹣8(舍弃),
∴点C的坐标为(2,4).


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】一条河的水流速度是1.8km/h,某条船在静水中的速度是akm/h,则该船在这条河中逆流行驶的速度是( )
A. (a+1.8)km/h B. (a﹣1.8)km/h
C. (a+3.6)km/h D. (a﹣3.6)km/h
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD. 
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=100°,∠D=30°,求∠AEM的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据调查,超速行驶是引发交通事故的主要原因之一.上周末,小明和三位同学用所学过的知识在一条笔直的道路上检测车速.如图,观测点C到公路的距离CD为100米,检测路段的起点A位于点C的南偏西60°方向上,终点B位于点C的南偏西45°方向上.某时段,一辆轿车由西向东匀速行驶,测得此车由A处行驶到B处的时间为4秒. 问此车是否超过了该路段16米/秒的限制速度?(参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,出租车是人们出行的一种便利交通工具,折线ABC是在我市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象.
(1)根据图象,当x≥3时y为x的一次函数,请写出函数关系式;
(2)某人乘坐13km,应付多少钱?
(3)若某人付车费42元,出租车行驶了多少千米?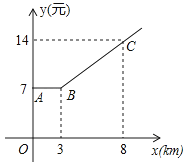
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,E,F,G,H分别为边AB,BC,CD,DA上的点,HA=EB=FC=GD,连接EG,FH,交点为O.
(1)如图2,连接EF,FG,GH,HE,试判断四边形EFGH的形状,并证明你的结论;
(2)将正方形ABCD沿线段EG,HF剪开,再把得到的四个四边形按图3的方式拼接成一个四边形.若正方形ABCD的边长为3cm,HA=EB=FC=GD=1cm,则图3中阴影部分的面积为多少?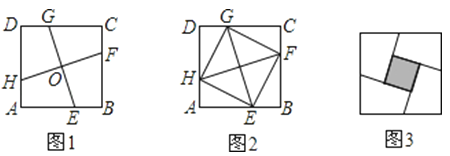
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com