
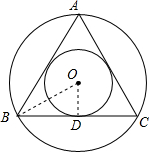
 已知,正三角形ABC的边长为1,正三角形ABC的外接圆和它的内切圆是同心圆,求这两个圆所形成的圆环的面积.
已知,正三角形ABC的边长为1,正三角形ABC的外接圆和它的内切圆是同心圆,求这两个圆所形成的圆环的面积. 分析 如图,△ABC为等边三角形,点O为中心,作OD⊥BC于D,连接BO,则BD=CD=$\frac{1}{2}$BC=$\frac{1}{2}$,利用等边三角形的性质得OB为△外接圆的半径,OD为内切圆的半径,由于OB2-OD2=BD2=$\frac{1}{4}$,然后利用圆的面积公式,计算两圆的面积差即可.
解答 解:如图,△ABC为等边三角形,点O为中心,
作OD⊥BC于D,连接BO,则BD=CD=$\frac{1}{2}$BC=$\frac{1}{2}$,
∵△ABC为等边三角形,
∴OB为△外接圆的半径,OD为内切圆的半径,
OB2-OD2=BD2=$\frac{1}{4}$,
∴这两个圆所形成的圆环的面积=π•OB2-π•OD2=$\frac{1}{4}$π.
点评 本题考查了三角形的内切圆与内心:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.也考查了三角形的外心和等边三角形的性质.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
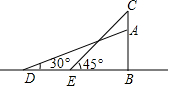 如图,小山AB的顶上有一高20m的铁塔(CA),在山脚平地上的D点,测得山顶A的仰角为30°,在E点测得塔尖C的仰角为45°(点D、E、B在一条直线上),已知DE=60m.求山高AB.(结果保留根号)
如图,小山AB的顶上有一高20m的铁塔(CA),在山脚平地上的D点,测得山顶A的仰角为30°,在E点测得塔尖C的仰角为45°(点D、E、B在一条直线上),已知DE=60m.求山高AB.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com