
【题目】如图,![]() 是
是![]() 的直径,且
的直径,且![]() ,点
,点![]() 为
为![]() 的延长线上一点,过点
的延长线上一点,过点![]() 作
作![]() 的切线
的切线![]() 、
、![]() ,切点分别为
,切点分别为![]() 、
、![]() .
.
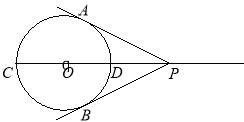
(1)、连接![]() ,若
,若![]() ,试证明
,试证明![]() 是等腰三角形;
是等腰三角形;
(2)、填空:①当![]() =
= ![]() 时,四边形
时,四边形![]() 是菱形;②当
是菱形;②当![]() =
= ![]() 时,四边形
时,四边形![]() 是正方形.
是正方形.
科目:初中数学 来源: 题型:
【题目】如图,已知直线AC∥BD,直线AB,CD不平行,点P在直线AB上,且和点A、B不重合.

(1)如图①,当点P在线段AB上时,若∠PCA=20°,∠PDB=30°,求∠CPD的度数;
(2)当点P在A、B两点之间运动时,∠PCA,∠PDB,∠CPD 之间满足什么样的等量关系?(直接写出答案)
(3)如图②,当点P在线段AB延长线上运动时,∠PCA,∠PDB,∠CPD 之间满足什么样的等量关系?并说明理由.
(4)当点P在线段BA延长线上运动时,∠PCA,∠PDB,∠CPD 之间满足什么样的等量关系?(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某弹簧的长度与所挂物体质量之间的关系如下表:
所挂物体的质量/千克 | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧的长度/厘米 | 10 | 10.4 | 10.8 | 11.2 | 11.6 | 12 |
(1)如果所挂物体的质量用x表示,弹簧的长度用y表示,请直接写出y与x满足的关系式.
(2)当所挂物体的质量为10千克时,弹簧的长度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
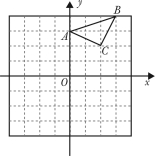
(1)、在网格内画出△ABC向下平移4个单位长度得到的![]() ,并写出点
,并写出点![]() 的坐标是 ;
的坐标是 ;
(2)、以点B为位似中心,在网格内画出![]() ,使
,使![]() 与△ABC位似,且位似比为2︰1,并写出点
与△ABC位似,且位似比为2︰1,并写出点![]() 的坐标是 ;
的坐标是 ;
(3)、![]() 的面积是 平方单位.
的面积是 平方单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把多项式分解因式,正确的结果是( )
A. 4a2+4a+1=(2a+1)2 B. a2﹣4b2=(a﹣4b)(a+b)
C. a2﹣2a﹣1=(a﹣1)2 D. (a﹣b)(a+b)=a2﹣b2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD是一张矩形纸片,AD=BC=1,AB=CD=5.在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK.
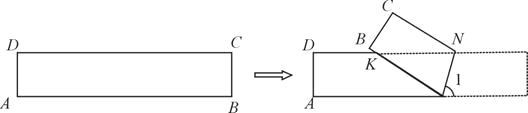

(1)若∠1=70°,求∠MKN的度数.
(2)△MNK的面积能否小于![]() ?若能,求出此时∠1的度数;若不能,试说明理由.
?若能,求出此时∠1的度数;若不能,试说明理由.
(3)如何折叠能够使△MNK的面积最大?请你利用备用图探究可能出现的情况,求出最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com