
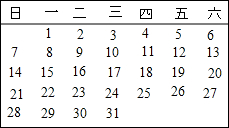
 如图是某月的月历,横着或竖着取连续的三个数字,它们的和可能是( )
如图是某月的月历,横着或竖着取连续的三个数字,它们的和可能是( )| A. | 18 | B. | 33 | C. | 38 | D. | 81 |
分析 分两种情形讨论:①若横着取连续是三个数字,设中间一个数为:x,则它左边的数是x-1,右边的数是x+1.
②若竖着且数,设中间一个数为y,则上面的数为y-7,下面的数为y+7.分别判断出不满足条件的数即可解决问题.
解答 解:①若横着取连续是三个数字,设中间一个数为:x,则它左边的数是x-1,右边的数是x+1,
由题意得x+x-1+x+1=3x,故一定是3的倍数,同时还要满足x不能在最左或最右,且x不能为1或31(因为1的左边没有数,31的右边没有数,它们不能做中间数)
所以x≠1、6、7、13、14、20、21、27、28、31,
所以3x≠3、18、21、39、42、60、63、81、84、93;
②若竖着且数,设中间一个数为y,则上面的数为y-7,下面的数为y+7,三个数的和为3y,即它们的和是一个能被3整除的正整数,同时还要满足y不能在最上行或最下行,且y不能为7,25,26,27(因为7的上面没有数,5,26,27的下面没有数,它们不能做中间数)
所以y≠1、2、3、4、5、6、7、25、26、27、28、29、30、31,
所以3y≠3、6、9、12、15、18、21、75、78、81、84、87、90、93;
综上所述,所取的三个数的和一定是3的倍数,它在3~93范围内,不能为3、18、21、81、84、93这6个数,
由此判断出A、D不符合题意,排除,而选项C中的数不能被3整除,也排除,选项B中的数33符合题意,
故选B.
点评 此题考查数字的变化规律,掌握日历表中数字的排列规律是解决问题的关键,学会用分类讨论的思想思考问题.


科目:初中数学 来源: 题型:解答题
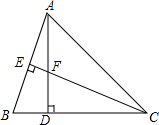 已知△ABC中,AD=CD,AD⊥BC,CE⊥AB,垂足分别为D,E,AD与CE相交于F点,且AE=$\frac{1}{2}$CF.求证:CE平分∠ACB.
已知△ABC中,AD=CD,AD⊥BC,CE⊥AB,垂足分别为D,E,AD与CE相交于F点,且AE=$\frac{1}{2}$CF.求证:CE平分∠ACB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
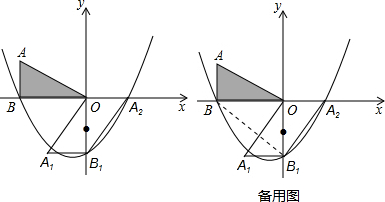
 如图,已知二次函数的图象关于x=-1对称,且最小值为-4,经过A(1,0)、B(0,-3)
如图,已知二次函数的图象关于x=-1对称,且最小值为-4,经过A(1,0)、B(0,-3)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com