
【题目】如图,已知点 A 、B分别在反比例函数 ![]() 的图象上,且OA ⊥OB ,则
的图象上,且OA ⊥OB ,则 ![]() 的值为( )
的值为( )
A.![]()
B.2
C.![]()
D.4
科目:初中数学 来源: 题型:
【题目】已知如图:AD∥BC,E、F分别在DC、AB延长线上.∠DCB=∠DAB,AE⊥EF,∠DEA=30°.

(1)求证:DC//AB.
(2)求∠AFE的大小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个口袋中放有290个涂有红、黑、白三种颜色的质地相同的小球.若红球个数是黑球个数的2倍多40个.从袋中任取一个球是白球的概率是![]() .
.
(1)求袋中红球的个数;
(2)求从袋中任取一个球是黑球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A1,A2,A3,…分别在x轴上,点B1,B2,B3,…分别在直线y=x上,△OA1B1,△B1A1A2,△B1B2A2,△B2A2A3,△B2B3A3…,都是等腰直角三角形,如果OA1=1,则点A2019的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【探究证明】某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.
(1)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.
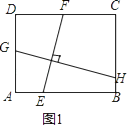
如图1,矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H.求证: ![]() =
= ![]() ;
;
(2)【结论应用】如图2,在满足(1)的条件下,又AM⊥BN,点M,N分别在边BC,CD上,若 ![]() =
= ![]() ,则
,则 ![]() 的值为;
的值为;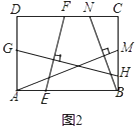
(3)【联系拓展】如图3,四边形ABCD中,∠ABC=90°,AB=AD=10,BC=CD=5,AM⊥DN,点M,N分别在边BC,AB上,求 ![]() 的值.
的值.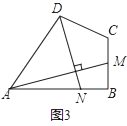
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)求直线BC的函数表达式;
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q,连接BM.
①若∠MBC=90°,求点P的坐标;
②若△PQB的面积为![]() ,请直接写出点M的坐标.
,请直接写出点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 问题解决:
问题解决:![]() 如图1,在平面直角坐标系xOy中,一次函数
如图1,在平面直角坐标系xOy中,一次函数![]() 与x轴交于点A,与y轴交于点B,以AB为腰在第二象限作等腰直角
与x轴交于点A,与y轴交于点B,以AB为腰在第二象限作等腰直角![]() ,
,![]() ,点A、B的坐标分别为A______、B______.
,点A、B的坐标分别为A______、B______.
![]() 求
求![]() 中点C的坐标.小明同学为了解决这个问题,提出了以下想法:过点C向x轴作垂线交x轴于点
中点C的坐标.小明同学为了解决这个问题,提出了以下想法:过点C向x轴作垂线交x轴于点![]() 请你借助小明的思路,求出点C的坐标;
请你借助小明的思路,求出点C的坐标;
![]() 类比探究:数学老师表扬了小明同学的方法,然后提出了一个新的问题,如图2,在平面直角坐标系xOy中,点A坐标
类比探究:数学老师表扬了小明同学的方法,然后提出了一个新的问题,如图2,在平面直角坐标系xOy中,点A坐标![]() ,点B坐标
,点B坐标![]() ,过点B作x轴垂线l,点P是l上一动点,点D是在一次函数
,过点B作x轴垂线l,点P是l上一动点,点D是在一次函数![]() 图象上一动点,若
图象上一动点,若![]() 是以点D为直角顶点的等腰直角三角形,请直接写出点D与点P的坐标.
是以点D为直角顶点的等腰直角三角形,请直接写出点D与点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明:
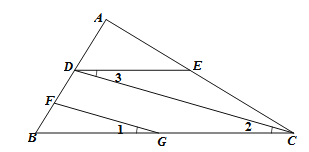
如图,FG//CD,∠1=∠3,∠B=50°,求∠BDE的度数.
解:∵FG//CD (已知)
∴∠2=_________( )
又∵∠1=∠3
∴∠3=∠_________( )
∴BC//__________( )
∴∠B+________=180°( )
又∵∠B=50°
∴∠BDE=130°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com