
【题目】如图,在正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上的一点,点
上的一点,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() 、
、![]() 、
、![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]()
![]() ,
,![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确的结论序号是( )
,其中正确的结论序号是( )
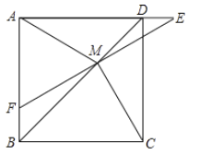
A.①②③B.①②④C.②③④D.①②③④
【答案】A
【解析】
①证明△AFM是等边三角形,可判断; ②③证明△CBF≌△CDE(ASA),可作判断; ④设MN=x,分别表示BF、MD、BC的长,可作判断.
解:①∵AM=EM,∠AEM=30°, ∴∠MAE=∠AEM=30°,
∴∠AMF=∠MAE+∠AEM=60°,
∵四边形ABCD是正方形, ∴∠FAD=90°,
∴∠FAM=90°-30°=60°,
∴△AFM是等边三角形,
∴FM=AM=EM, 故①正确;
②连接CE、CF, ∵四边形ABCD是正方形, ∴∠ADB=∠CDM,AD=CD,
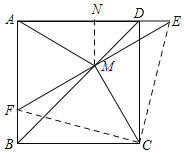
在△ADM和△CDM中,
∵ 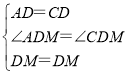 ,
,
∴△ADM≌△CDM(SAS), ∴AM=CM,
∴FM=EM=CM, ∴∠MFC=∠MCF,∠MEC=∠ECM,
∵∠ECF+∠CFE+∠FEC=180°, ∴∠ECF=90°,
∵∠BCD=90°, ∴∠DCE=∠BCF,
在△CBF和△CDE中,
∵ 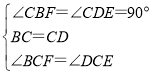 ,
,
∴△CBF≌△CDE(ASA), ∴BF=DE; 故②正确;
③∵△CBF≌△CDE, ∴CF=CE, ∵FM=EM, ∴CM⊥EF, 故③正确;
④过M作MN⊥AD于N, 设MN=![]() ,则AM=AF=
,则AM=AF=![]() ,
,

![]() ,DN=MN=
,DN=MN=![]() , ∴AD=AB=
, ∴AD=AB= ![]() ,
,
∴DE=BF=AB-AF=![]() ,
,
∴ ![]() ,
,
∵BC=AD= ![]() , 故④错误;
, 故④错误;
所以本题正确的有①②③;
故选:A.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】设一次函数y=kx+b(k,b是常数,k≠0)的图象过A(1,3),B(﹣1,﹣1)两点.
(1)求该一次函数的表达式;
(2)若点(2a+2,a2)在该一次函数图象上,求a的值.
(3)已知点C(x1,y1)和点D(x2,y2)在该一次函数图象上,设m=(x1﹣x2)(y1﹣y2),判断反比例函数y=![]() 的图象所在的象限,说明理由.
的图象所在的象限,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名运动员同时从![]() 地出发前往
地出发前往![]() 地,在笔直的公路上进行骑自行车训练如图所示,反映了甲、乙两名运动员在公路上进行训练时的行驶路程
地,在笔直的公路上进行骑自行车训练如图所示,反映了甲、乙两名运动员在公路上进行训练时的行驶路程![]() (千米)与行驶时间
(千米)与行驶时间![]() (小时)之间的关系,下列四种说法:①甲的速度为40千米/小时;②乙的速度始终为50千米/小时;③行驶1小时时,乙在甲前10千米处;④甲、乙两名运动员相距5千米时,
(小时)之间的关系,下列四种说法:①甲的速度为40千米/小时;②乙的速度始终为50千米/小时;③行驶1小时时,乙在甲前10千米处;④甲、乙两名运动员相距5千米时,![]() 或
或![]() .其中正确的个数有( )
.其中正确的个数有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
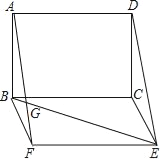
【题目】如图,已知矩形ABCD和BCEF,AF=BE,AF与BE交于点G,∠AGB=60°.
(1)求证:AF=DE;
(2)若AB=6,BC=8,求AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
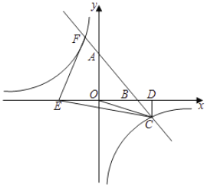
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于第二、四象限的
的图象交于第二、四象限的![]() 、
、![]() 两点,与
两点,与![]() 、
、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,过点
两点,过点![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() ,且
,且![]() 的面积为3,作点
的面积为3,作点![]() 关于
关于![]() 轴对称点
轴对称点![]() .
.
(1)求一次函数和反比例函数的解析式;
(2)连接![]() 、
、![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕A逆时针方向旋转40°得到△ADE,点B经过的路径为弧BD,是图中阴影部分的面积为( )

A. ![]() π﹣6 B.
π﹣6 B. ![]() π C.
π C. ![]() π﹣3 D.
π﹣3 D. ![]() +π
+π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有三个完全相同的小球,分别标有数字3、4、5.从袋子中随机取出一个小球,用小球上的数字作为十位的数字,然后放回;再取出一个小球,用小球上的数字作为个位上的数字,这样组成一个两位数,试问:按这种方法能组成哪些位数?十位上的数字与个位上的数字之和为9的两位数的概率是多少?用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
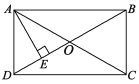
【题目】如图,在矩形ABCD中,对角线AC与BD交于点O,且△ADO为等边三角形,过点A作AE⊥BD于点E.
(1)求∠ABD的度数;
(2)若BD=10,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com