
已知:如图1,在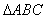 中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别是D、E,连接DE。
中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别是D、E,连接DE。
(1) 求∠AED的度数.
(2) ①求证:EB-EC= DE
DE
②若点A为直线AB上的动点,当点A运动到如图2位置时,①中的结论是否成立,若成立,说明理由;若不成立,直接写出类似的结论(不必证明)。
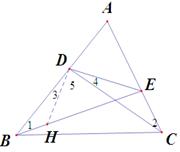
(3) 若点A运动到BD的延长线时,如图3所示,当DC=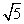 ,DE=2
,DE=2 时(0<BE<2),求AE的长。
时(0<BE<2),求AE的长。
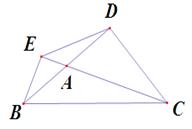
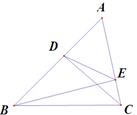
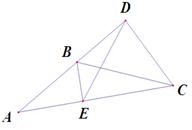
图1 图2 图3
(1)解:如图1:∵ CD⊥AB,BE⊥AC,垂足分别是D、E.
∴∠AEB=∠ADC=90°
∵∠A=∠A
∴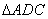 ∽
∽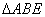
∴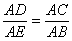
∴ 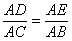
又∵∠A=∠A
∴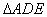 ∽
∽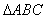
 ∴∠AED=∠ABC=45°
∴∠AED=∠ABC=45°
图1 图2
(2)①证明:如图2:在BE上截取BH=EC
∵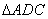 ∽
∽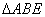
∴∠1=∠2
∵CD⊥AB
∴∠BDC=90°且∠ABC=45°
∴BD=DC
在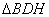 和
和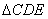 中
中
 ∵ BD=DC,∠1=∠2 ,BH=EC
∵ BD=DC,∠1=∠2 ,BH=EC
∴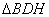 ≌
≌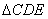 (SAS)
(SAS)
∴DH=DE ∠3=∠4
∵∠3+∠5=90°
∴∠HDE=∠4+∠5=90°
∴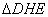 为等腰直角三角形
为等腰直角三角形
∴BE-EC=BE-BH=HE= DE
DE
∴BE - EC= DE
DE
②如图2,原结论不成立,,结论应为:EC-BE= DE
DE
(3)如图3:延长EB到H,使BH=EC
同理可证: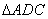 ∽
∽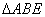 ,
,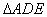 ∽
∽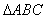
∠DEC=45° ∴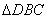 为等腰直角三角形
为等腰直角三角形
∵∠1=∠2=∠DCE
BD=DC
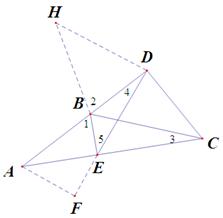 BH=EC
BH=EC
∴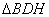 ≌
≌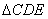 (SAS)
(SAS)
∴DE=DH
∴∠5=180°-90°-45°=45°
∴∠5=∠H=45°
∴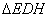 为等腰直角三角形
为等腰直角三角形
∴HB+BE=EC+BE=HB= DE 图3
DE 图3
∴EC+BE= DE
DE
设BE=x
∵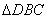 为等腰直角三角形
为等腰直角三角形
∴BC= DC=
DC=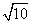
∵EC+BE= DE 即EC+X=
DE 即EC+X= ·
·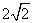 =4
=4
∴EC=4-X
在Rt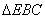 中,由勾股定理得:
中,由勾股定理得:
解得:X=1或3
∵ 0<BE<2
∴ BE=1 (如图3)
∴tan∠3=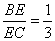
延长DE,过点A作AF⊥DE的延长线于点F
在Rt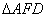 中,tan∠4= tan∠3=
中,tan∠4= tan∠3=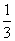
∵∠AEF=∠DEC=45°
∴设AF=EF=a 则DF=3a
∴ DE=3a-a=2a=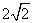
∴ a=
∴AE= ·
· =2
=2


科目:初中数学 来源: 题型:
在平面直角坐标系中,反比例函数与二次函数y=k(x2+x-1)的图象交于点A(1,k)和点B(-1,-k).
(1)当k=-2时,求反比例函数的解析式;
(2)已知经过原点O的两条直线AB与CD分别与双曲线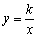 (k>0)交于A、B和C、D,那么AB与CD互相平分,所以四边形ACBD是平行四边形.
(k>0)交于A、B和C、D,那么AB与CD互相平分,所以四边形ACBD是平行四边形.
问:平行四边形ABCD能否成为矩形?能否成为正方形?若能,请说明直线AB、CD的位置关系;若不能,请说明理由
(3)设二次函数的图象的顶点为Q,当△ABQ是以AB为斜边的直角三角形时,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
某校举行了“洁美家园”的演讲比赛,赛后整理参赛同学的成绩,将学生的成绩分成 A、B、C、D四个等级,并制成了如下的条形统计图和扇形图(如图1、图2).
(1)补全条形统计图.
(2)学校决定从本次比赛中获得A和B的学生中各选出一名去参加市中学生环保演讲比赛.已知A等中男生有2名,B等中女生有3 名,请你用“列表法”或“树形图法”的方法求出所选两位同学恰好是一名男生和一名女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
某班级学生参加初三体育考试,其中有20名同学参加了排球发球考试,裁判将发球过网个数记入下表,由于不小心弄脏了表格,有两个数据看不到. 则下列说法中正确的是( )
| 过网个数 | 6 | 7 | 8 | 9 | 10 |
| 人数 | 3 | 2 | 5 |
A.这组数据众数是8 B.这组数据的中位数是7.5
C.这组数据的方差是4 D.这组数据的平均数P满足8.1<P<8.6
查看答案和解析>>
科目:初中数学 来源: 题型:
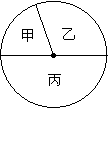
某校某校初一新生来自甲、乙、丙三个小学,其人数比为2:3:5,如图所示的扇形图表示上述分布情况.已知来自甲小学的学生为180人,则下列说法不正确的是( )
A.扇形甲的圆心角是72°
B.学生的总人数是900人
C.丙小学的人数比乙小学的人数多180人
D.甲小学的人数比丙小学的人数少180人
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com