【答案】
分析:A、举一反例,即可得到本选项为假命题;
B、根据立方根的定义:一个负数只有一个负的立方根,即可作出判断;
C、举一个反例,圆周率π为无理数,它的平方仍为无理数,本选项为假命题;
D、根据题意画出图形,写出已知,求证,利用等腰三角形的性质,等边对等角得到一对角相等,再根据垂直得到一对直角相等,又一对公共边,利用AAS即可得到三角形全等,从而得证,本选项为真命题.
解答: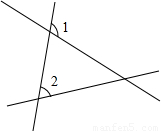
解:A、根据题意画出图形,如图所示:
如图:∠1和∠2是一对同位角,但根据外角性质得到∠1>∠2,故同位角不一定相等,本选项为假命题;
B、∵

=-

,∴-

的立方根为-

,本选项为假命题;
C、若a是无理数为π,π
2也是无理数,本选项为假命题;
D、根据题意画出图形,如图所示:

已知:△ABC中,AB=AC,CD⊥AB,BE⊥AC,
求证:CD=BE.
证明:∵AB=AC,
∴∠ABC=∠ACB,
又CD⊥AB,BE⊥AC,
∴∠CDB=∠BEC=90°,
在△BDC和△CEB中,
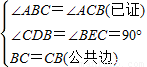
,
∴△BDC≌△CEB(AAS),
∴CD=BE,
即等腰三角形两腰上的高相等,本选项为真命题.
故选D.
点评:此题综合考查了同位角,内错角及同旁内角,立方根的定义,无理数的运算,全等三角形的判定与性质以及等腰三角形的性质,解题的关键是要掌握若说明一个命题为假命题,只需举一个反例即可;若说明命题为真命题,必须经过严格的证明.

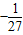 的立方根是±
的立方根是±
 解:A、根据题意画出图形,如图所示:
解:A、根据题意画出图形,如图所示: =-
=- ,∴-
,∴- 的立方根为-
的立方根为- ,本选项为假命题;
,本选项为假命题;
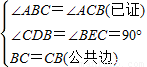 ,
,

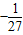 的立方根是±
的立方根是±