
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,过
,过![]() ,
,![]() ,
,![]() 三点作圆,点
三点作圆,点![]() 在第一象限部分的圆上运动,连结
在第一象限部分的圆上运动,连结![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 的延长线于点
的延长线于点![]() ,下列说法:①
,下列说法:①![]() ;②
;②![]() ;③
;③![]() 的最大值为10.其中正确的是( )
的最大值为10.其中正确的是( )
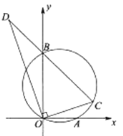
A. ①②B. ②③C. ①③D. ①②③
【答案】C
【解析】
连接AB,由题意得AB为圆的直径,根据同角的余角相等可得∠AOC=∠BOD,根据圆周角定理得∠OCB=∠OAB,可推出∠OBA=∠D,根据勾股定理求出AB,可出sin∠D的值,证出△OCD∽△OAB,则![]() ,OC取最大值等于直径时CD的值最大.
,OC取最大值等于直径时CD的值最大.
解:连接AB,
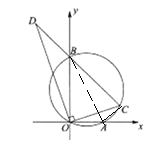
∵∠DOC=90°,∠BOA=90°,
∴∠BOD+∠BOC=90°,∠AOC+∠BOC =90°,
∴∠AOC=∠BOD,①正确;
∵∠DOC=90°,∠BOA=90°,
∴∠OCB+∠D=90°,∠OAB+∠OBA =90°,
∵∠OCB=∠OAB,
∴∠OBA=∠D,
∵OA=2,OB=4,AB=![]() ,
,
∴sin∠D=sin∠OBA=![]() ,②错误;
,②错误;
∵∠DOC=∠BOA=90°,∠OCB=∠OAB,
∴△OCD∽△OAB,
∴![]()
∵∠BOA=90°,
∴AB为圆的直径,
∴OC取最大值等于直径AB时CD的值最大,
∴CD的最大值![]() ,③正确.
,③正确.
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连接CF并延长交AB于点M,MN⊥CM交射线AD于点N
(1)如图1,当点F为BE的中点时,求证:AM=CE;
(2)如图2,若![]() =
=![]() =n(n≥3)时,请直接写出
=n(n≥3)时,请直接写出![]() 的值;
的值;
(3)若矩形ABCD(AB>BC)对角线AC交MN于T,H为边BC上一点,∠CMH=45°且![]() =
=![]() (如图3).若CF平分∠ACB,请直接写出
(如图3).若CF平分∠ACB,请直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),B(3,0).下列结论:①2a﹣b=0;②(a+c)2<b2;③当﹣1<x<3时,y<0;④当a=1时,将抛物线先向上平移2个单位,再向右平移1个单位,得到抛物线y=(x﹣2)2﹣2.其中正确的是( )
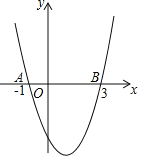
A. ①③ B. ②③ C. ②④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成(1)~(3)题:
数学课上,老师出示了这样一道题:
如图1,△ABC中,AB=AC,∠BAC=90°,点D是BC的中点,E是AC的中点,经过点A、C作射线BE的垂线,垂足分别为点F、G,连接AG.探究线段DF和AG的关系.某学习小组的同学经过思考后,交流了自己的想法:
小明:“经过观察和度量,发现∠ABF和∠ACG相等.”小刚:“经过观察和度量,发现有两条线段和AF相等.”
小伟:“通过构造全等三角形,经过进一步推理,可以得到线段DF和AG的关系.”
……
老师:“若点E不是AC的中点,其他条件不变(如图2),可以求出![]() 的值.”
的值.”
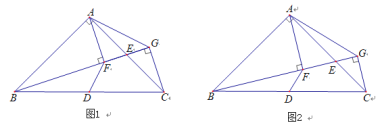
(1)求证:AF=FG;
(2)探究线段DF和AG的关系,并证明;
(3)直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄石市在创建国家级文明卫生城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A种,B种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象顶点坐标为(1,4),且经过点C(3,0).
(1)求该二次函数的解析式;
(2)当x取何值时,y随x的增大而减小?
(3)当![]() 时,直接写出x的取值范围.
时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD为台球桌面,AD=260cm,AB=130cm,球目前在E点位置,AE=60cm.如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“美丽泰州”的工作部署,市政府计划对城区道路进行改造,现安排甲、乙两个工程队完成该改造工作.已知甲队的工作效率是乙队工作效率的![]() 倍,甲队改造720米的道路比乙队改造同样长的道路少用4天.
倍,甲队改造720米的道路比乙队改造同样长的道路少用4天.
(1)甲、乙两工程队每天能改造道路的长度分别是多少米?
(2)若甲队工作一天需付费用7万元,乙队工作一天需付费用5万元,若需改造的道路全长2400米,改造总费用不超过195万元,则至少安排甲队工作多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com