
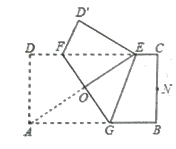
【题目】如图,矩形纸片ABCD中,AD= 1,AB一2.将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB、CD交于点G、F,AE与FG交于点仪当触ED的外接圆与BC相切于BC的中点N.则折痕FG的长为________
【答案】![]()
【解析】试题解析:设AE与FG的交点为O.
根据轴对称的性质,得AO=EO.
取AD的中点M,连接MO.
则MO=![]() DE,MO∥DC.
DE,MO∥DC.
设DE=x,则MO=![]() x,
x,
在矩形ABCD中,∠C=∠D=90°,
∴AE为△AED的外接圆的直径,O为圆心.
延长MO交BC于点N,则ON∥CD.
∴∠CNM=180°-∠C=90°.
∴ON⊥BC,四边形MNCD是矩形.
∴MN=CD=AB=2.∴ON=MN-MO=2-![]() x.
x.
∵△AED的外接圆与BC相切,
∴ON是△AED的外接圆的半径.
∴OE=ON=2-![]() x,AE=2ON=4-x.
x,AE=2ON=4-x.
在Rt△AED中,AD2+DE2=AE2,
∴12+x2=(4-x)2.
解这个方程,得x=![]() .
.
∴DE=![]() ,OE=2-
,OE=2-![]() x=
x=![]() .
.
根据轴对称的性质,得AE⊥FG.
∴∠FOE=∠D=90°.可得FO=![]() .
.
又AB∥CD,∴∠EFO=∠AGO,∠FEO=∠GAO.
∴△FEO≌△GAO.∴FO=GO.
∴FG=2FO=![]() .
.
∴折痕FG的长是![]() .
.


科目:初中数学 来源: 题型:
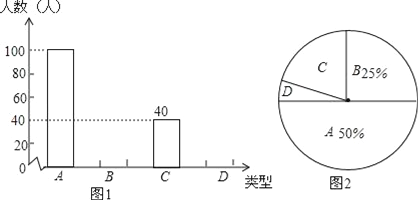
【题目】中学生上学带手机的现象越来越受到社会的关注,为此媒体记者随机调查了某校若干名学生上学带手机的目的,分为四种类型:A接听电话;B收发短信;C查阅资料;D游戏聊天.并将调查结果绘制成图1和图2的统计图(不完整),请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图1、图2补充完整;
(3)现有4名学生,其中A类两名,B类两名,从中任选2名学生,求这两名学生为同一类型的概率(用列表法或树状图法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个正五棱柱的底面边长为2cm,高为4cm。

(1)这个棱柱共有多少个面?计算它的侧面积;
(2)这个棱柱共有多少个顶点?有多少条棱?
(3)试用含有![]() 的代数式表示
的代数式表示![]() 棱柱的顶点数、面数、与棱的条数。
棱柱的顶点数、面数、与棱的条数。
查看答案和解析>>
科目:初中数学 来源: 题型:
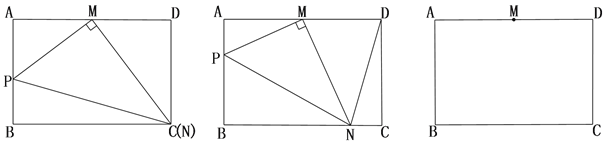
【题目】在矩形ABCD中,AB=4,AD=6,M是AD边的中点,P是射线AB上的一个动点(不与A、B重合),MN⊥PM交射线BC于N点.
(1)如图1,当点N与点C重合时,求:AP的长;
(2)如图2,在点N的运动过程中,求证: ![]() 为定值;
为定值;
(3)在射线AB上,是否存在点P,使得![]() ∽
∽![]() ,若存在,求此时AP的长;若不存在,请说明理由.
,若存在,求此时AP的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com