
 如图,某一时刻一根2米长的竹竿EF影长GE为1.2米,此时,小红测得一棵被风吹斜的杨树与地面成30°角,树顶端B在地面上的影子点D与B到垂直地面的落点C的距离是3.6米,则树长AB等于12米.
如图,某一时刻一根2米长的竹竿EF影长GE为1.2米,此时,小红测得一棵被风吹斜的杨树与地面成30°角,树顶端B在地面上的影子点D与B到垂直地面的落点C的距离是3.6米,则树长AB等于12米. 分析 先利用△BDC∽△FGE得到$\frac{BC}{3.6}$=$\frac{2}{1.2}$,可计算出BC=6,然后在Rt△ABC中利用含30度的直角三角形三边的关系即可得到AB的长.
解答 解:如图,CD=3.6m,
∵△BDC∽△FGE,
∴$\frac{BC}{CD}$=$\frac{EF}{GE}$,即$\frac{BC}{3.6}$=$\frac{2}{1.2}$,
∴BC=6,
在Rt△ABC中,∵∠A=30°,
∴AB=2BC=12,
即树长AB是12米.
故答案为12.
点评 本题考查了相似三角形的应用:利用影长测量物体的高度;利用相似测量河的宽度(测量距离);借助标杆或直尺测量物体的高度.


 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案科目:初中数学 来源: 题型:解答题
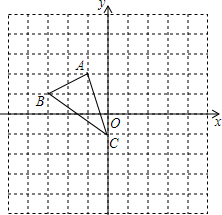 如图,在平面直角坐标系网格中,△ABC的顶点都在格点上,点C坐标(0,-1).
如图,在平面直角坐标系网格中,△ABC的顶点都在格点上,点C坐标(0,-1).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
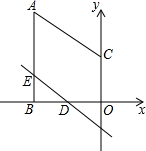 如图在平面直角坐标系内,点A与点C的坐标分别为(-4,8),(0,5),过点A作AB⊥x轴于点B,过OB上的动点D作直线y=kx+b平行于AC,与AB相交于点E,连结CD,过点E作直线EF∥CD,交AC于点F.
如图在平面直角坐标系内,点A与点C的坐标分别为(-4,8),(0,5),过点A作AB⊥x轴于点B,过OB上的动点D作直线y=kx+b平行于AC,与AB相交于点E,连结CD,过点E作直线EF∥CD,交AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 20 | B. | 23 | C. | 25 | D. | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一条公路修到湖边时,需拐弯绕道而过,如果第一次拐的角∠A是100°第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是( )
如图,一条公路修到湖边时,需拐弯绕道而过,如果第一次拐的角∠A是100°第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是( )| A. | 120° | B. | 130° | C. | 140° | D. | 150° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com