
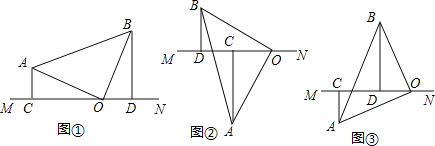
【题目】在△ABC中![]() ,AO=BO,直线MN经过点O, 且AC⊥MN于C,BD⊥MN于D
,AO=BO,直线MN经过点O, 且AC⊥MN于C,BD⊥MN于D
(1) 当直线MN绕点O旋转到图①的位置时,求证:CD=AC+BD;
(2) 当直线MN绕点O旋转到图②的位置时,求证:CD=AC-BD;
(3) 当直线MN绕点O旋转到图③的位置时,试问:CD、AC、BD有怎样的等量关系?请写出这个等量关系,并加以证明。
【答案】(1)证明见解析;(2)证明见解析;(3)CD=BD-AC,证明见解析.
【解析】试题分析:(1)通过证明△ACO≌△ODB得到OC=BD,AC=OD,则CD=AC+BD;
(2)通过证明△ACO≌△ODB得到OC=BD,AC=OD,则CD=AC-BD;
(3)通过证明△ACO≌△ODB得到OC=BD,AC=OD,则CD=BD-AC.
试题解析:(1)如图1,
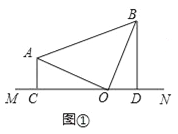
∵△AOB中,∠AOB=90°,
∴∠AOC+∠BOD=90°,
直线MN经过点O,且AC⊥MN于C,BD⊥MN于D,
∴∠ACO=∠BDO=90°
∴∠AOC+∠OAC=90°,
∴∠OAC=∠BOD,
在△ACO和△ODB中,
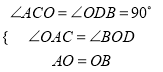
∴△ACO≌△ODB(AAS),
∴OC=BD,AC=OD,
∴CD=AC+BD;
(2)如图2,
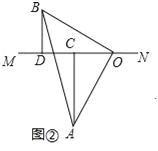
∵△AOB中,∠AOB=90°,
∴∠AOC+∠BOD=90°,
直线MN经过点O,且AC⊥MN于C,BD⊥MN于D,
∴∠ACO=∠BDO=90°
∴∠AOC+∠OAC=90°,
∴∠OAC=∠BOD,
在△ACO和△ODB中,
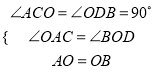 ,
,
∴△ACO≌△ODB(AAS),
∴OC=BD,AC=OD,
∴CD=OD﹣OC=AC﹣BD,即CD=AC﹣BD.
(3)如图3,
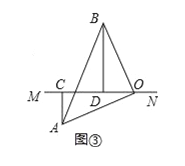
∵△AOB中,∠AOB=90°,
∴∠AOC+∠BOD=90°,
直线MN经过点O,且AC⊥MN于C,BD⊥MN于D,
∴∠ACO=∠BDO=90°
∴∠AOC+∠OAC=90°,
∴∠OAC=∠BOD,
在△ACO和△ODB中,
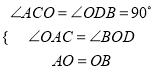 ,
,
∴△ACO≌△ODB(AAS),
∴OC=BD,AC=OD,
∴CD=OC﹣OD=BD﹣AC,
即CD=BD﹣AC.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】在上,下行的轨道上,两列火车相向而行,甲列车长235m,速度108 km/h,乙列车长260m,速度为90 km/h.这两列火车从车头相遇到车尾离开需要( )秒.
A. 9 B. 10 C. 11 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表一和图一:
(1)请将表一和图一中的空缺部分补充完整.
(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图二(没有弃权票,每名学生只能推荐一个),请计算每人的得票数.
(3)若每票计1分,系里将笔试、口试、得票三项测试得分按![]() 的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标中,点P(1,﹣3)关于x轴的对称点坐标是( )
A. (1,﹣3) B. (﹣1,3) C. (﹣1,﹣3) D. (1,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆出租车从A地出发,在一条东西走向的街道上往返,每次行驶的路程(记向东为正)记录如下(x>9且x<26,单位:km)

(1)说出这辆出租车每次行驶的方向.
(2)求经过连续4次行驶后,这辆出租车所在的位置.
(3)这辆出租车一共行驶了多少路程?
查看答案和解析>>
科目:初中数学 来源: 题型:
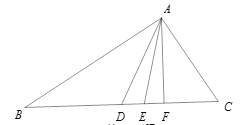
【题目】如图所示,三亚有三个车站A、B、C成三角形,一辆公共汽车从B站前往到C站。
(1)当汽车运动到点D时,刚好BD=CD,连接AD,AD这条线段是什么线段?这样的线段在△ABC中有几条?此时有面积相等的三角形吗?
(2)汽车继续向前运动,当运动到点E时,发现∠BAE=∠CAE,那么AE这条线段是什么线段?在△ABC中,这样的线段又有几条?
(3)汽车继续向前运动,当运动到点F时,发现∠AFB=∠AFC=90°,则AF是什么线段?在△ABC中,这样的线段有几条?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句中,正确的有( )
①相等的圆心角所对的弧相等;
②平分弦的直径垂直于弦;
③长度相等的两条弧是等弧;
④经过圆心的每一条直线都是圆的对称轴.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com