
分析 (1)根据点A、B、C的坐标写出有向向量即可;
(2)求出向量AB,AC的模,向量AB,AC的数量积,再由向量的夹角公式,即可求出.
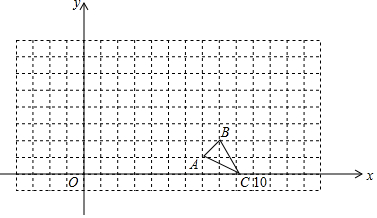
解答 解:(1)∵A(1,0),B(0,1),C(2,5).
∴$\overrightarrow{AB}$=(0-1,1-0)=(-1,1),$\overrightarrow{AC}$=(2-1,5-0)=(1,5).
(2)|$\overrightarrow{AB}$|=$\sqrt{(-1)^{2}+{1}^{2}}$=$\sqrt{2}$,|$\overrightarrow{AC}$|=$\sqrt{{1}^{2}+{5}^{2}}$=$\sqrt{26}$,$\overrightarrow{AB}$•$\overrightarrow{AC}$=(-1)×1+1×5=4.
则cosθ=$\frac{\overrightarrow{AB}•\overrightarrow{AC}}{|\overrightarrow{AB}||\overrightarrow{AC}|}$=$\frac{2\sqrt{13}}{\sqrt{13}}$,
所以向量$\overrightarrow{AB}$与$\overrightarrow{AC}$的夹角θ=arccos$\frac{2\sqrt{13}}{\sqrt{13}}$.
点评 本题考查平面向量的运算和向量的模,以及向量的数量积的坐标表示,和夹角公式,考查运算能力.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
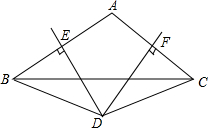 如图,在△ABC中,DE垂直平分AB,DF垂直平分AC.
如图,在△ABC中,DE垂直平分AB,DF垂直平分AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
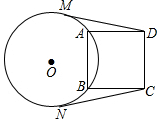 如图,以⊙O的弦AB为边向圆外作正方形ABCD,分别过点D、C作⊙O的切线DM、CN,切点分别为M、N.
如图,以⊙O的弦AB为边向圆外作正方形ABCD,分别过点D、C作⊙O的切线DM、CN,切点分别为M、N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一根旗杆在离地面9m处断裂,旗杆顶部落在离旗杆底部12m处,将旗杆接好后,由于台风影响,旗杆再次断裂,已知旗杆的顶部落在距离旗杆底部6m处,问旗杆第二次是在离地面多少米处断裂的?
如图,一根旗杆在离地面9m处断裂,旗杆顶部落在离旗杆底部12m处,将旗杆接好后,由于台风影响,旗杆再次断裂,已知旗杆的顶部落在距离旗杆底部6m处,问旗杆第二次是在离地面多少米处断裂的?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
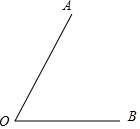 如图,∠AOB,用直尺圆规按下列要求作图
如图,∠AOB,用直尺圆规按下列要求作图查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com