
”¾ĢāÄæ”æŌŚÕż·½ŠĪABCDÖŠ£¬¶Ō½ĒĻßAC£¬BD½»ÓŚµćO£¬µćPŌŚĻ߶ĪBCÉĻ£Ø²»ŗ¬µćB£©£¬”ĻBPE£½![]() ”ĻACB£¬PE½»BOÓŚµćE£¬¹żµćB×÷BF”ĶPE£¬“¹×ćĪŖF£¬½»ACÓŚµćG£®
”ĻACB£¬PE½»BOÓŚµćE£¬¹żµćB×÷BF”ĶPE£¬“¹×ćĪŖF£¬½»ACÓŚµćG£®
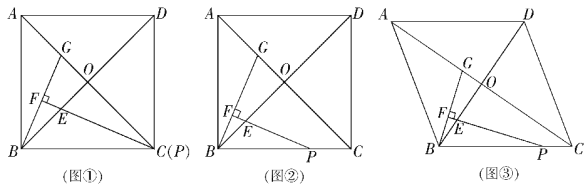
£Ø1£© µ±µćPÓėµćCÖŲŗĻŹ±£ØČēĶ¼¢Ł£©£®ĒóÖ¤£ŗ”÷BOG”Õ”÷POE£»£Ø4·Ö£©
£Ø2£©Ķعż¹Ū²ģ”¢²āĮ攢²ĀĻė£ŗ![]() = £¬²¢½įŗĻĶ¼¢ŚÖ¤Ć÷ÄćµÄ²ĀĻė£»£Ø5·Ö£©
= £¬²¢½įŗĻĶ¼¢ŚÖ¤Ć÷ÄćµÄ²ĀĻė£»£Ø5·Ö£©
£Ø3£©°ŃÕż·½ŠĪABCDøÄĪŖĮāŠĪ£¬ĘäĖūĢõ¼ž²»±ä£ØČēĶ¼¢Ū£©£¬Čō”ĻACB=¦Į£¬Ēó![]() µÄÖµ£®£ØÓĆŗ¬¦ĮµÄŹ½×Ó±ķŹ¾£©£Ø5·Ö£©
µÄÖµ£®£ØÓĆŗ¬¦ĮµÄŹ½×Ó±ķŹ¾£©£Ø5·Ö£©
”¾“š°ø”æ£Ø1£©Ö¤Ć÷¼ū½āĪö£Ø2£©![]() £¬Ö¤Ć÷¼ū½āĪö£Ø3£©
£¬Ö¤Ć÷¼ū½āĪö£Ø3£©![]()
”¾½āĪö”æ½ā£ŗ£Ø1£©Ö¤Ć÷£ŗ”ßĖıߊĪABCDŹĒÕż·½ŠĪ£¬PÓėCÖŲŗĻ£¬
”ąOB=OP £¬ ”ĻBOC=”ĻBOG=90”ć”£
”ßPF”ĶBG £¬”ĻPFB=90”ć£¬”ą”ĻGBO=90”ć”Ŗ”ĻBGO£¬”ĻEPO=90”ć”Ŗ”ĻBGO”£
”ą”ĻGBO=”ĻEPO ”£”ą”÷BOG”Õ”÷POE£ØAAS£©”£
£Ø2£©![]() ”£Ö¤Ć÷ČēĻĀ£ŗ
”£Ö¤Ć÷ČēĻĀ£ŗ
ČēĶ¼£¬¹żP×÷PM//AC½»BGÓŚM£¬½»BOÓŚN£¬
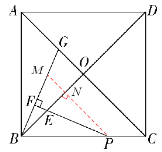
”ą”ĻPNE=”ĻBOC=900£¬ ”ĻBPN=”ĻOCB”£
”ß”ĻOBC=”ĻOCB =450£¬ ”ą ”ĻNBP=”ĻNPB”£
”ąNB=NP”£
”ß”ĻMBN=900”Ŗ”ĻBMN£¬ ”ĻNPE=900”Ŗ”ĻBMN£¬”ą”ĻMBN=”ĻNPE”£
”ą”÷BMN”Õ”÷PEN£ØASA£©”£”ąBM=PE”£
”ß”ĻBPE=![]() ”ĻACB£¬”ĻBPN=”ĻACB£¬”ą”ĻBPF=”ĻMPF”£
”ĻACB£¬”ĻBPN=”ĻACB£¬”ą”ĻBPF=”ĻMPF”£
”ßPF”ĶBM£¬”ą”ĻBFP=”ĻMFP=900”£
ÓÖ”ßPF=PF£¬ ”ą”÷BPF”Õ”÷MPF£ØASA£©”£”ąBF=MF £¬¼“BF=![]() BM”£
BMӣ
”ąBF=![]() PE£¬ ¼“
PE£¬ ¼“![]() ”£
ӣ
£Ø3£©ČēĶ¼£¬¹żP×÷PM//AC½»BGÓŚµćM£¬½»BOÓŚµćN£¬
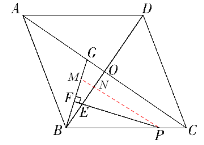
”ą”ĻBPN=”ĻACB=¦Į£¬”ĻPNE=”ĻBOC=900”£
ÓÉ£Ø2£©Ķ¬ĄķæɵĆBF=![]() BM£¬ ”ĻMBN=”ĻEPN”£
BM£¬ ”ĻMBN=”ĻEPN”£
”ß”ĻBNM=”ĻPNE=900£¬”ą”÷BMN”×”÷PEN”£
”ą![]() ”£
ӣ
ŌŚRt”÷BNPÖŠ£¬![]() £¬ ”ą
£¬ ”ą![]() £¬¼“
£¬¼“![]() ”£
ӣ
”ą![]() ”£
ӣ
£Ø1£©ÓÉÕż·½ŠĪµÄŠŌÖŹæÉÓÉAASÖ¤µĆ”÷BOG”Õ”÷POE”£
£Ø2£©¹żP×÷PM//AC½»BGÓŚM£¬½»BOÓŚN£¬ĶعżASAÖ¤Ć÷”÷BMN”Õ”÷PENµĆµ½BM=PE£¬ĶعżASAÖ¤Ć÷”÷BPF”Õ”÷MPFµĆµ½BF=MF£¬¼“æÉµĆ³ö![]() µÄ½įĀŪ”£
µÄ½įĀŪ”£
£Ø3£©¹żP×÷PM//AC½»BGÓŚµćM£¬½»BOÓŚµćN£¬Ķ¬£Ø2£©Ö¤µĆBF=![]() BM£¬ ”ĻMBN=”ĻEPN£¬“Ó¶ųæÉÖ¤µĆ”÷BMN”×”÷PEN£¬ÓÉ
BM£¬ ”ĻMBN=”ĻEPN£¬“Ó¶ųæÉÖ¤µĆ”÷BMN”×”÷PEN£¬ÓÉ![]() ŗĶRt”÷BNPÖŠ
ŗĶRt”÷BNPÖŠ![]() ¼“æÉĒóµĆ
¼“æÉĒóµĆ![]() ”£
ӣ



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĀÖ“¬“Ó¼×µŲĖ³Ė®æŖĶłŅŅµŲ£¬ĖłÓĆŹ±¼ä±Č“ÓŅŅµŲÄęĖ®æŖĶł¼×µŲÉŁ1.5Š”Ź±”£ŅŃÖŖ“¬ŌŚ¾²Ė®ÖŠµÄĖŁ¶ČĪŖ18Ē§Ć×Ć抔Ź±£¬Ė®Į÷ĖŁ¶ČĪŖ2Ē§Ć×Ć抔Ź±£¬Ēó¼×ŅŅĮ½µŲÖ®¼äµÄ¾ąĄė£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Rt”÷ABCµÄŠ±±ßABŌŚxÖįÉĻ£¬AB=4£¬µćAµÄ×ų±źĪŖ£Ø-1,0£©£¬µćCŌŚyÖįµÄÕż°ėÖį”£ČōÅ×ĪļĻßy=ax2+bx+c (a”Ł0)µÄĶ¼Ļń¾¹żµćA,B,C£¬ŌņÅ×ĪļĻߵıķ“ļŹ½ĪŖ__________£»ČōŅŌ¶ÆÖ±Ļßl:y=-![]() x+mĪŖ¶Ō³ĘÖį£¬Ļ߶ĪBC¹ŲÓŚÖ±ĻßlµÄ¶Ō³ĘĻ߶ĪBCÓė¶ž“ĪŗÆŹżĶ¼ĻńÓŠ½»µć£¬ŌņmµÄȔֵ·¶Ī§ŹĒ__________.
x+mĪŖ¶Ō³ĘÖį£¬Ļ߶ĪBC¹ŲÓŚÖ±ĻßlµÄ¶Ō³ĘĻ߶ĪBCÓė¶ž“ĪŗÆŹżĶ¼ĻńÓŠ½»µć£¬ŌņmµÄȔֵ·¶Ī§ŹĒ__________.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£¬ČēĶ¼£¬AC”ĶBC£¬HF”ĶAB£¬CD”ĶAB£¬”Ļ1Óė”Ļ2»„²¹£®ĒóÖ¤£ŗDE”ĶAC£® 
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖAM”ĪCN£¬µćBĪŖĘ½ĆęÄŚŅ»µć£¬AB”ĶBCÓŚB£® 
£Ø1£©ČēĶ¼1£¬Ö±½ÓŠ“³ö”ĻAŗĶ”ĻCÖ®¼äµÄŹżĮæ¹ŲĻµ£»
£Ø2£©ČēĶ¼2£¬¹żµćB×÷BD”ĶAMÓŚµćD£¬ĒóÖ¤£ŗ”ĻABD=”ĻC£»
£Ø3£©ČēĶ¼3£¬ŌŚ£Ø2£©ĪŹµÄĢõ¼žĻĀ£¬µćE”¢FŌŚDMÉĻ£¬Į¬½ÓBE”¢BF”¢CF£¬BFĘ½·Ö”ĻDBC£¬BEĘ½·Ö”ĻABD£¬Čō”ĻFCB+”ĻNCF=180”ć£¬”ĻBFC=3”ĻDBE£¬Ēó”ĻEBCµÄ¶ČŹż£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æµŲĒņµÄĘ½¾ł°ė¾¶Ō¼ĪŖ6 371 000Ć×£¬øĆŹż×ÖÓĆæĘѧ¼ĒŹż·ØæɱķŹ¾ĪŖ£Ø””””£©
A.0.6371”Į107
B.6.371”Į106
C.6.371”Į107
D.6.371”Į103
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£ŗČēĶ¼£¬ABCDÖŠ£¬E”¢F·Ö±šŹĒAD£¬BCµÄÖŠµć£®ĒóÖ¤£ŗ 
£Ø1£©”÷AFB”Õ”÷CED£»
£Ø2£©ĖıߊĪAECFŹĒĘ½ŠŠĖıߊĪ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»øöÕż³£µÄČĖÄÜ»ī1 000 000·ÖÖÓĀš£æ“š£ŗ________£ØĢī”°ÄÜ”±»ņ”°²»ÄÜ”±£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼ĘĖć£Ø©1£©2n+£Ø©1£©2n+1µÄÖµŹĒ£Ø £©
A.2
B.©2
C.”Ą2
D.0
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com