
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
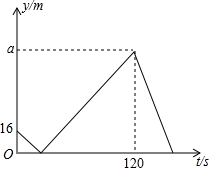 甲、乙两人在直线道路上同起点、同终点、同方向,分别以不同的速度匀速跑步600米,先到终点的人原地休息.已知甲先出发4秒后,乙才出发,在跑步的整个过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则a的值为104.
甲、乙两人在直线道路上同起点、同终点、同方向,分别以不同的速度匀速跑步600米,先到终点的人原地休息.已知甲先出发4秒后,乙才出发,在跑步的整个过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则a的值为104.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,四边形ABCD中,点F在边AD上,BF的延长线交CD的延长线于E点,下列式子中能推出AD∥BC的式子是( )
如图,四边形ABCD中,点F在边AD上,BF的延长线交CD的延长线于E点,下列式子中能推出AD∥BC的式子是( )| A. | FD•EC=ED•BC | B. | AF•EF=BF•DF | C. | EF•EC=ED•BE | D. | AB•FD=DE•AF |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
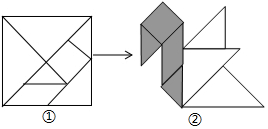 用边长为1的正方形纸板,制成一副七巧板(如图①),将它拼成“小天鹅”图案(如图②),其中阴影部分的面积为 ( )
用边长为1的正方形纸板,制成一副七巧板(如图①),将它拼成“小天鹅”图案(如图②),其中阴影部分的面积为 ( )| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{7}{16}$ | D. | $\frac{3}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +5 | -2 | -4 | +13 | -10 | +16 | -9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com