
【题目】如图,AB是⊙O的直径,AC是⊙O的弦,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E,连接BD.
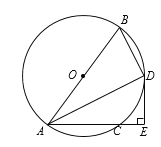
(1)求证:DE是⊙O的切线;
(2)若BD=3,AD=4,则DE= .
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OD,如图,先证明OD∥AE,再利用DE⊥AE得到OD⊥DE,然后根据切线的判定定理得到结论;
(2)证明△ABD∽△ADE,通过线段比例关系求出DE的长.
(1)证明:连接OD
∵AD平分∠BAC
∴∠BAD=∠DAC
∵OA=OD
∴∠BAD=∠ODA
∴∠ODA=∠DAC
∴OD∥AE
∴∠ODE+∠E=180°
∵DE⊥AE
∴∠E=90°
∴∠ODE=180°-∠E=180°-90°=90°,即OD⊥DE
∵点D在⊙O上
∴DE是⊙O的切线.

(2)∵AB是⊙O的直径,
∴∠ADB=90°,
∵AD平分∠BAC,
∴∠BAD=∠DAE,
在△ABD和△ADE中,
![]() ,
,
∴△ABD∽△ADE,
∴![]() ,
,
∵BD=3,AD=4,AB=![]() =5
=5
∴DE=![]() =
=![]() .
.


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】作图题:⊙O上有三个点A,B,C,∠BAC=70°,请画出要求的角,并标注.
(1)画一个140°的圆心角;(2)画一个110°的圆周角;(3)画一个20°的圆周角.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读以下材料,并完成相应的任务:
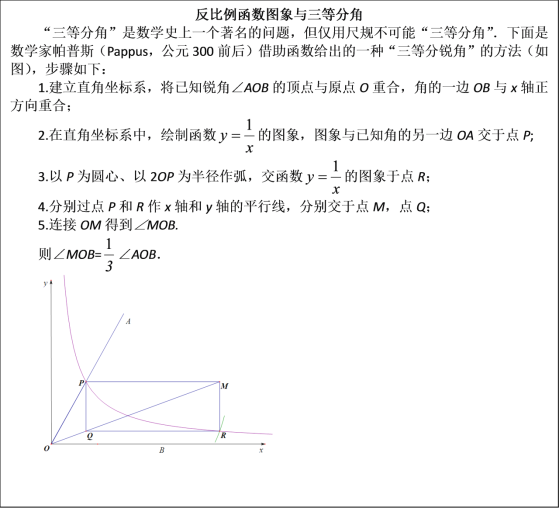
任务:
(1)设P(a,![]() ),R(b,
),R(b,![]() ),求直线OM的函数解析式(用含a,b的代数式表示),并说明Q点在直线OM上;
),求直线OM的函数解析式(用含a,b的代数式表示),并说明Q点在直线OM上;
(2)证明:∠MOB=![]() ∠AOB.
∠AOB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代城市绿化带在不断扩大,绿化用水的节约是一个非常重要的问题.


如图1、图2所示,某喷灌设备由一根高度为0.64 m的水管和一个旋转喷头组成,水管竖直安装在绿化带地面上,旋转喷头安装在水管顶部(水管顶部和旋转喷头口之间的长度、水管在喷灌区域上的占地面积均忽略不计),旋转喷头可以向周围喷出多种抛物线形水柱,从而在绿化带上喷灌出一块圆形区域.现测得喷的最远的水柱在距离水管的水平距离3 m处达到最高,高度为1 m.
(1)求喷灌出的圆形区域的半径;
(2)在边长为16 m的正方形绿化带上固定安装三个该设备,喷灌区域可以完全覆盖该绿化带吗?如果可以,请说明理由;如果不可以,假设水管可以上下调整高度,求水管高度为多少时,喷灌区域恰好可以完全覆盖该绿化带.(以上需要画出示意图,并有必要的计算、推理过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD,对角线AC、BD相交于点O,AC=6,BD=8.点E是AB边上一点,求作矩形EFGH,使得点F、G、H分别落在边BC、CD、AD上.设 AE=m.

(1)如图①,当m=1时,利用直尺和圆规,作出所有满足条件的矩形EFGH;(保留作图痕迹,不写作法)
(2)写出矩形EFGH的个数及对应的m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E,D是线段BE上的一个动点,则![]() 的最小值是( )
的最小值是( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 10
D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”小长假期间,某超市为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”、“30元”的字样.规定:顾客在本超市一次性购物满500元以上均可获得两次摸球的机会(摸出小球后放回).超市根据两小球所标金额的和返还相应的代金券.
(1)顾客甲购物1000元,则他最少可获 元代金券,最多可获 元代金券.
(2)请用树形图或列表方法,求出顾客甲获得不低于30元(含30元)代金券的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AB=5,AC=3,D是AB的中点,E是直线BC上一点,把△BDE沿直线ED翻折后,点B落在点F处,当FD⊥BC时,线段BE的长为_____.
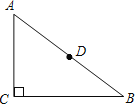
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com