
【题目】在□ABCD中,E为BC的中点,过点E作EF⊥AB于点F,延长DC,交FE的延长线于点G,连结DF,已知∠FDG=45°
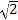
(1)求证:GD=GF.
(2)已知BC=10, ![]() .求 CD的长.
.求 CD的长.
【答案】(1)证明见解析;
(2)CD长为5
【解析】试题分析:(1)由ABCD是平行四边形得:AB∥CD,又因为EF⊥AB,所以∠ DGF=∠GFB=90°,在△DGF中,求得∠FDG=∠DFG=45° ,再根据等角对等边得到GD=GF;
(2)由![]() 且
且 ![]() 得:GF=8,又由 BC=10 ,点E 是BC中点,则CE=5,由ABCD是平行四边形 得: ∠ GCE=∠EBF,则△EBF≌△ECG,所以GE=4 ,在在 Rt△CGE 中
得:GF=8,又由 BC=10 ,点E 是BC中点,则CE=5,由ABCD是平行四边形 得: ∠ GCE=∠EBF,则△EBF≌△ECG,所以GE=4 ,在在 Rt△CGE 中 ![]() 所以CG=3, CD=8-3=5;
所以CG=3, CD=8-3=5;
试题解析:
(1)证明:
∵EF⊥AB,
∴∠GFB=90°
∵ABCD是平行四边形
∴AB∥CD, ∠ DGF=∠GFB=90°
在△DGF中,已知∠FDG=45°
∴∠DFG=45°
∴∠FDG=∠DFG
∴GD=GF
(2)解:由(1)得![]() 又
又 ![]()
∴![]()
∴GF=8
∵ BC=10 ,点E 是BC中点
∴CE=5
∵ABCD是平行四边形
∴ ∠ GCE=∠EBF
在△EBF和△ECG中
∠ EFB=∠ECG=90°
CE=EB=5
∴△EBF≌△ECG
∴GE=4
在 Rt△CGE 中 ![]()
∴CG=3
∴CD=8-3=5


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】某厂家以A、B两种原料,利用不同的工艺手法生产出了甲、乙两种袋装产品,其中,甲产品每袋含1.5千克A原料、1.5千克B原料;乙产品每袋含2千克A原料、1千克B原料.甲、乙两种产品每袋的成本价分别为袋中两种原料的成本价之和.若甲产品每袋售价72元,则利润率为20%.某节庆日,厂家准备生产若干袋甲产品和乙产品,甲产品和乙产品的数量和不超过100袋,会计在核算成本的时候把A原料和B原料的单价看反了,后面发现如果不看反,那么实际成本比核算时的成本少500元,那么厂家在生产甲乙两种产品时实际成本最多为_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区为改善生态环境,实行生活垃圾的分类处理,将生活垃圾分成三类:厨房垃圾、可回收垃圾和其他垃圾,分别记为![]() ,并且设置了相应的垃圾箱“厨房垃圾”箱,“可回收垃圾”箱和“其他垃圾”箱,分别记为
,并且设置了相应的垃圾箱“厨房垃圾”箱,“可回收垃圾”箱和“其他垃圾”箱,分别记为![]() .
.
(1)为了了解居民生活垃圾分类投放的情况,现随机抽取了小区三类垃圾箱中总共![]() 吨生活垃圾,数据统计如下图(单位:吨):
吨生活垃圾,数据统计如下图(单位:吨):
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
请根据以上信息,估计“厨房垃圾”投放正确的概率;
(2)若将三类垃圾随机投入三类垃圾箱,请用画树状图或列表格的方法求出垃圾投放正确的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上(不与端点重合),
上(不与端点重合),![]() ,射线
,射线![]() 交
交![]() 延长线于点
延长线于点![]() ,点
,点![]() 在直线
在直线![]() 上,
上,![]() .
.
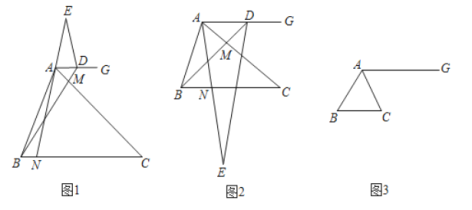
(1)(观察猜想)如图1,点![]() 在射线
在射线![]() 上,当
上,当![]() 时,
时,
①线段![]() 与
与![]() 的数量关系是______;
的数量关系是______;
②![]() 的度数是______;
的度数是______;
(2)(探究证明)如图2点![]() 在射线
在射线![]() 上,当
上,当![]() 时,判断并证明线段
时,判断并证明线段![]() 与
与![]() 的数量关系,求
的数量关系,求![]() 的度数;
的度数;
(3)(拓展延伸)如图3,点![]() 在直线
在直线![]() 上,当
上,当![]() 时,
时,![]() ,点
,点![]() 是
是![]() 边上的三等分点,直线
边上的三等分点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,请直接写出线段
,请直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=﹣x2+bx+c(c>0)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB=OC=3,顶点为M.
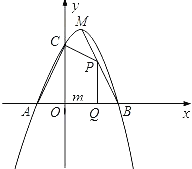
(1)求二次函数的解析式;
(2)点P为线段BM上的一个动点,过点P作x轴的垂线PQ,垂足为Q,若OQ=m,四边形ACPQ的面积为S,求S关于m的函数解析式,并写出m的取值范围;
(3)探索:线段BM上是否存在点N,使△NMC为等腰三角形?如果存在,求出点N的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在双曲线y=的第一象限的那一支上,AB垂直于x轴与点B,
点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE
的面积为3,则k的值为 ▲ .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com