
ЁОЬтФПЁПШчЭМЃЌЪ§жсЩЯЃЌЕу A ЕФГѕЪМЮЛжУБэЪОЕФЪ§ЮЊ 1ЃЌЯжЕу A зіШчЯТвЦЖЏЃКЕк 1 ДЮЕу A ЯђзѓвЦЖЏ 3 ИіЕЅЮЛГЄЖШжСЕу A1ЃЌЕк 2 ДЮДгЕу A1 ЯђгввЦЖЏ 6 ИіЕЅЮЛГЄЖШжСЕу A2ЃЌЕк 3 ДЮДгЕу A2 ЯђзѓвЦЖЏ 9 ИіЕЅЮЛГЄЖШжСЕу A3ЃЌЁЃЌАДееетжжвЦЖЏЗНЪННјааЯТШЅЃЌЕу A4 БэЪОЕФЪ§ЃЌЪЧ__________ ЃЌШчЙћЕу An гыдЕуЕФОрРыВЛаЁгк 20ЃЌ ФЧУД n ЕФзюаЁжЕЪЧ________________ ЃЎ
![]()
ЁОД№АИЁП7ЃЌ13ЃЎ
ЁОНтЮіЁП
ЪдЬтЕквЛДЮЕуAЯђзѓвЦЖЏ3ИіЕЅЮЛГЄЖШжСЕуA1ЃЌдђA1БэЪОЕФЪ§ЃЌ1Љ3=Љ2Љ2ЃЛ
Ек2ДЮДгЕуA1ЯђгввЦЖЏ6ИіЕЅЮЛГЄЖШжСЕуA2ЃЌдђA2БэЪОЕФЪ§ЮЊЉ2+6=4ЃЛ
Ек3ДЮДгЕуA2ЯђзѓвЦЖЏ9ИіЕЅЮЛГЄЖШжСЕуA3ЃЌдђA3БэЪОЕФЪ§ЮЊ4Љ9=Љ5ЃЛ
Ек4ДЮДгЕуA3ЯђгввЦЖЏ12ИіЕЅЮЛГЄЖШжСЕуA4ЃЌдђA4БэЪОЕФЪ§ЮЊЉ5+12=7ЃЛ
Ек5ДЮДгЕуA4ЯђзѓвЦЖЏ15ИіЕЅЮЛГЄЖШжСЕуA5ЃЌдђA5БэЪОЕФЪ§ЮЊ7Љ15=Љ8ЃЛ
ЁЃЛ
дђA7БэЪОЕФЪ§ЮЊЉ8Љ3=Љ11ЃЌA9БэЪОЕФЪ§ЮЊЉ11Љ3=Љ14ЃЌA11БэЪОЕФЪ§ЮЊЉ14Љ3=Љ17ЃЌA13БэЪОЕФЪ§ЮЊЉ17Љ3=Љ20ЃЌ
A6БэЪОЕФЪ§ЮЊ7+3=10ЃЌA8БэЪОЕФЪ§ЮЊ10+3=13ЃЌA10БэЪОЕФЪ§ЮЊ13+3=16ЃЌA12БэЪОЕФЪ§ЮЊ16+3=19ЃЌ
ЫљвдЕуAnгыдЕуЕФОрРыВЛаЁгк20ЃЌФЧУДnЕФзюаЁжЕЪЧ13ЃЎ
ЙЪД№АИЮЊЃК7ЃЌ13ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуEдквдABЮЊжБОЖЕФЁбOЩЯЃЌЕуCЪЧ ![]() ЕФжаЕуЃЌЙ§ЕуCзїCDДЙжБгкAEЃЌНЛAEЕФбгГЄЯпгкЕуDЃЌСЌНгBEНЛACгкЕуFЃЎ
ЕФжаЕуЃЌЙ§ЕуCзїCDДЙжБгкAEЃЌНЛAEЕФбгГЄЯпгкЕуDЃЌСЌНгBEНЛACгкЕуFЃЎ 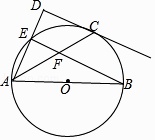
ЃЈ1ЃЉЧѓжЄЃКCDЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєcosЁЯCAD= ![]() ЃЌBF=15ЃЌЧѓACЕФГЄЃЎ
ЃЌBF=15ЃЌЧѓACЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНааЫФБпаЮABCDжаЃЌEЃЌFЮЊBCЩЯСНЕуЃЌЧвBE=CFЃЌAF=DEЃЎ
ЧѓжЄЃКЃЈ1ЃЉЁїABFЁеЁїDCEЃЛ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПДгЙВЯэЕЅГЕЃЌЙВЯэЦћГЕЕШЙВЯэГіааЕНЙВЯэгъЩЁЕШЙВЯэЮяЦЗЃЌИїЪНИїбљЕФЙВЯэ
ОМУФЃЪНдкИїИіСьгђбИЫйЕФЦеМАЁЃ
(1) ЮЊЛёЕУЬЉжнЪаЪаУёВЮгыЙВЯэОМУЕФЛюЖЏаХЯЂЃЌЯТСаЕїВщЗНЪНжаБШНЯКЯРэЕФЪЧЁЁ ЁЁЃЛ
AЃЎЖдФГбЇаЃЕФШЋЬхЭЌбЇНјааЮЪОэЕїВщ BЃЎЖдФГаЁЧјЕФзЁЛЇНјааЮЪОэЕїВщ
CЃЎдкШЋЪаРяЕФВЛЭЌЧјЯиЃЌбЁШЁВПЗжЪаУёНјааЮЪОэЕїВщ
(2) ЕїВщаЁзщЫцЛњЕїВщСЫЬЉаЫЪаЪаУёЦяЙВЯэЕЅГЕЧщПіЃЌФГЩчЧјФъСфдк12ЁЋ36ЫъЕФШЫга1000ШЫЃЌДгжаЫцЛњГщШЁСЫ100ШЫЃЌЭГМЦСЫЫћУЧЦяЙВЯэЕЅГЕЕФШЫЪ§ЃЌВЂЛцжЦСЫШчЯТВЛЭъећЕФЭГМЦЭМБэЃЎ

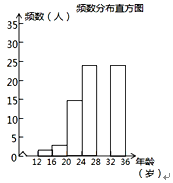
ИљОнвдЩЯаХЯЂНтД№ЯТСаЮЪЬтЃК
Ђй ЧѓГіЭГМЦБэжаЕФaЁЂbЃЌВЂВЙШЋЦЕЪ§ЗжВМжБЗНЭМ
Ђк ЪдЙРМЦетИіЩчЧјФъСфдк20ЫъЕН32Ыъ(КЌ20ЫъЃЌВЛКЌ32Ыъ)ЦяЙВЯэЕЅГЕЕФШЫгаЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЪЧе§ЗНаЮЃЌЕуEЪЧЦНУцФквьгкЕуAЕФШЮвтвЛЕуЃЌвдЯп
ЖЮAEЮЊБпзїе§ЗНаЮAEFGЃЌСЌНгEBЃЌGDЃЎ
(1) ШчЭМ1ЃЌХаЖЯEBгыGDЕФЙиЯЕВЂЫЕУїРэгЩЃЛ
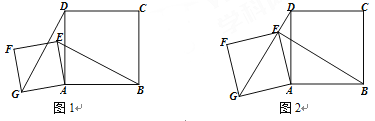
(2) ШчЭМ2ЃЌШєЕуEдкЯпЖЮDGЩЯЃЌABЃН5ЃЌAGЃН3![]() ЃЌЧѓBEЕФГЄЃЎ
ЃЌЧѓBEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЭЙЮхБпаЮABCDEЕФБпГЄОљЯрЕШЃЌЧвЁЯDBE=ЁЯABE+ЁЯCBDЃЌAC=1ЃЌдђBDБиЖЈТњзуЃЈ ЃЉ 
A.BDЃМ2
B.BD=2
C.BDЃО2
D.вдЩЯЧщПіОљгаПЩФм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПББОЉЕиЬњ1КХЯпЪЧжаЙњзюдчЕФЕиЬњЯпТЗЃЌ2000ФъЪЕЯжСЫ23ИіГЕеОЕФЙсЭЈдЫгЊЃЌИУЯпЮїЦ№ЦЛЙћдАеОЃЌЖЋжСЫФЛнЖЋеОЃЌШЋГЄдМ31ЧЇУзЃЎЯТБэЪЧББОЉЕиЬњ1КХЯпЪзФЉГЕЪБПЬБэЃЌПЊЭљЫФЛнЖЋЗНЯђКЭЦЛЙћдАЗНЯђЕФЪзГЕЕФЦНОљЫйЖШОљЮЊУПаЁЪБ60ЧЇУзЃЌЧѓгЩЦЛЙћдАеОКЭЫФЛнЖЋеОПЊГіЕФЪзГЕЕквЛДЮЯргіЕФЪБМфЃЎ
ББОЉЕиЬњ1КХЯпЪзФЉГЕЪБПЬБэ | ||||
ГЕеОУћГЦ | ЭљЫФЛнЖЋЗНЯђ | ЭљЦЛЙћдАЗНЯђ | ||
ЪзГЕЪБМф | ФЉГЕЪБМф | ЪзГЕЪБМф | ФЉГЕЪБМф | |
ЦЛЙћдА | 5ЃК10 | 22ЃК55 | -- | -- |
Ё | Ё | Ё | Ё | Ё |
ЫФЛнЖЋ | -- | -- | 5ЃК05 | 23ЃК15 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНтЗНГЬ![]() Љ1ЕФВНжшШчЯТЃК
Љ1ЕФВНжшШчЯТЃК
ЃЈНтЮіЃЉЕквЛВНЃК![]() Љ1ЃЈЗжЪ§ЕФЛљБОаджЪЃЉ
Љ1ЃЈЗжЪ§ЕФЛљБОаджЪЃЉ
ЕкЖўВНЃК2xЉ1ЃН3ЃЈ2x+8ЃЉЉ3ЁЁЃЈЂйЃЉ
ЕкШ§ВНЃК2xЉ1ЃН6x+24Љ3ЁЁЃЈЂкЃЉ
ЕкЫФВНЃК2xЉ6xЃН24Љ3+1ЁЁЃЈЂлЃЉ
ЕкЮхВНЃКЉ4xЃН22ЃЈЂмЃЉ
ЕкСљВНЃКxЃНЉ![]() ЁЁЃЈЂнЃЉ
ЁЁЃЈЂнЃЉ
вдЩЯНтЗНГЬЕкЖўВНЕНЕкСљВНЕФМЦЫувРОнгаЃКЂйШЅРЈКХЗЈдђЃЎЂкЕШЪНаджЪвЛЃЎЂлЕШЪНаджЪЖўЃЎЂмКЯВЂЭЌРрЯюЗЈдђЃЎЧыбЁдёХХађЭъШЋе§ШЗЕФвЛИібЁЯюЃЈЁЁЁЁЃЉ
A. ЂкЂйЂлЂмЂк B. ЂкЂйЂлЂмЂл C. ЂлЂйЂкЂмЂл D. ЂлЂйЂмЂкЂл
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаТНЈГЩбЇаЃОйааУРЛЏТЬЛЏаЃдАЛюЖЏЃЌОХФъМЖМЦЛЎЙКТђAЃЌBСНжжЛЈФОЙВ100ПУТЬЛЏВйГЁЃЌЦфжаAЛЈФОУППУ50дЊЃЌBЛЈФОУППУ100дЊЃЎ
ЃЈ1ЃЉШєЙКНјAЃЌBСНжжЛЈФОИеКУгУШЅ8000дЊЃЌдђЙКТђСЫAЃЌBСНжжЛЈФОИїЖрЩйПУЃП
ЃЈ2ЃЉШчЙћЙКТђBЛЈФОЕФЪ§СПВЛЩйгкAЛЈФОЕФЪ§СПЃЌЧыЩшМЦвЛжжЙКТђЗНАИЪЙЫљашзмЗбгУзюЕЭЃЌВЂЧѓГіИУЙКТђЗНАИЫљашзмЗбгУЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com