
 如图,梯形ABCD中,AD∥BC,E为BC上任意一点,连接AE、DE、G1、G2、G3分别为△ABE,△ADE,△DEC的重心,BC=2AD=12,梯形的高为6,则△G1G2G3的面积为
如图,梯形ABCD中,AD∥BC,E为BC上任意一点,连接AE、DE、G1、G2、G3分别为△ABE,△ADE,△DEC的重心,BC=2AD=12,梯形的高为6,则△G1G2G3的面积为| 1 |
| 3 |
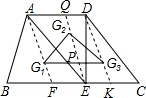 解:连接AG1,并延长交BC于点F,连接DG3,并延长交BC于点K,连接EG2,并延长交AD于点Q,交G1G3于点P,
解:连接AG1,并延长交BC于点F,连接DG3,并延长交BC于点K,连接EG2,并延长交AD于点Q,交G1G3于点P,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 如图,已知△ABC:
如图,已知△ABC:查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,正方形A1B1C1D1可看成是分别以A、B、C、D为位似中心将正方形ABCD放大一倍得到的图形(正方形ABCD的边长放大到原来的3倍),由正方形ABCD到正方形A1B1C1D1,我们称之作了一次变换,再将正方形A1B1C1D1作一次变换就得到正方形A2B2C2D2,…,依此下去,作了2005次变换后得到正方形A2005B2005C2005D2005,若正方形ABCD的面积是1,那么正方形A2005B2005C2005D2005的面积是多少( )
如图,正方形A1B1C1D1可看成是分别以A、B、C、D为位似中心将正方形ABCD放大一倍得到的图形(正方形ABCD的边长放大到原来的3倍),由正方形ABCD到正方形A1B1C1D1,我们称之作了一次变换,再将正方形A1B1C1D1作一次变换就得到正方形A2B2C2D2,…,依此下去,作了2005次变换后得到正方形A2005B2005C2005D2005,若正方形ABCD的面积是1,那么正方形A2005B2005C2005D2005的面积是多少( )| A、32005 |
| B、32004 |
| C、34010 |
| D、34009 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、相离 | B、相交 | C、相切 | D、不确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:
A、
| ||
B、-
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:

| A、AB∥CD |
| B、AD∥BC |
| C、∠ADB=∠BDC |
| D、∠ADB>∠BDC |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com