
【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根x1 , x2 . 求实数k的取值范围.
科目:初中数学 来源: 题型:
【题目】某饮料厂生产一种饮料,经测算,用1吨水生产的饮料所获利润y(元)是1吨水的价格x(元)的一次函数.
(1)根据下表提供的数据,求y与x的函数关系式;当水价为每吨10元时,1吨水生产出的饮料所获的利润是多少?
1吨水价格x(元) | 4 | 6 |
用1吨水生产的饮料所获利润y(元) | 200 | 198 |
(2)为节约用水,这个市规定:该厂日用水量不超过20吨时,水价为每吨4元;日用水量超过20吨时,超过部分按每吨40元收费.已知该厂日用水量不少于20吨,设该厂日用水量为t吨,当日所获利润为W元,求W与t的函数关系式;该厂加强管理,积极节水,使日用水量不超过25吨,但仍不少于20吨,求该厂的日利润的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面给出的正多边形的边长都是20cm,请分别按下列要求设计一种剪拼方法(用虚线表示你的设计方案,把剪拼线段用粗黑实线,在图中标注出必要的符号和数据,并作简要说明. 
(1)将图1中的正方形纸片剪拼成一个底面是正方形的直四棱柱模型,使它的表面积与原正方形面积相等;
(2)将图2中的正三角形纸片剪拼成一个底面是正三角形的直三棱柱模型,使它的表面积与原正三角形的面积相等;
(3)将图3中的正五边形纸片剪拼成一个底面是正五边形的直五棱柱模型,使它的表面积与原正五边形的面积相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABCD中,E、F分别是边BC , CD上的点,且EF∥BD , AE、AF分别交BD与点G和点H , BD=12,EF=8.求: 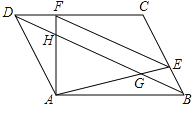
(1)![]() 的值;
的值;
(2)线段GH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王大爷家有一块梯形形状土地,如图,AD∥BC , 对角线AD , BC相交于点O , 王大爷量得AD长3米,BC长9米,王大爷准备在△AOD处种大白菜,那么王大爷种大白菜的面积与整个土地的面积比为( ).
A.1:14
B.3:14
C.1:16
D.3:16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,E、D分别是AC、BC的中点,AD、BE交于点O , 则S△DOE:S△AOB=( ) 
A.1:2
B.2:3
C.1:3
D.1:4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一组管道如图1所示,其中四边形ABCD是矩形,O是AC的中点,管道由AB,BC,CD,DA,OA,OB,OC,OD组成,在BC的中点M 处放置了一台定位仪器.一个机器人在管道内匀速行进,对管道进行检测.设机器人行进的时间为x,机器人与定位仪器之间的距离为y,表示y与x的函数关系的图象大致如图2所示,则机器人的行进路线可能为( )
A.A→O→D
B.B→O→D
C.A→B→O
D.A→D→O
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com