练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．已知三角形的三边分别为3，x，4，那么最长边x的取值范围是4≤x＜7．

    分析 根据三角形的任意两边之和大于第三边，两边之差小于第三边的取值范围，再根据x是最长边求解即可．

    解答 解：由三角形的三边关系定理可得：
    4-3＜x＜4+3，
    即1＜x＜7．
    又∵x是三角形中最长的边，
    ∴4≤x＜7．
    故答案为：4≤x＜7．

    点评 此题主要考查了三角形的三边关系定理，三角形中第三边的范围是：大于已知的两边的差，而小于已知两边的和．解题时需要注意：x是三角形最长边的条件，这是本题最容易出错的地方．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    6．已知A，B，C三地位置如图所示，∠C=90°，A，C两地的距离是4km，B，C两地的距离是3km，则A，B两地的距离是5km．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．已知两个变量x，y之间的关系式为y=（a-2）x2+（b+2）x-3．
    （1）当a≠2时，x，y之间是二次函数关系；
    （2）当a=2且b≠2时，x，y之间是一次函数关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．下列说法正确的是（　　）
    A．零是正数不是负数B．不是正数的数一定是负数
    C．零既是正数也是负数D．零既不是正数也不是负数

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

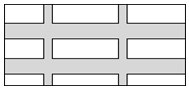    11．如图，要设计一幅宽20厘米，长30厘米的图案，其中有两横两竖的彩条，横、竖彩条的宽度比为2：1，如果要使彩条所占面积是图案面积的一半，那么竖彩条宽度是多少？若设竖彩条宽度是x厘米，则根据题意可列方程（30-2x）（20-4x）=300．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．某特技飞行队在名胜风景旅游区做特技表演，其中一架飞机起飞后的高度变化如表：
    高度变化上升4.5km下降3.2km上升1.1km下降1.4km
    记作+4.5km-3.2km+1.1km-1.4km
    （1）此时这架飞机比起飞点高了多少千米？
    （2）如果飞机每上升或下降1千米需消耗2升燃油，那么这架飞机在这4个动作表演过程中，一共消耗了多少升燃油？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．学校组织一次乒乓球赛，要求每两队之间都要赛一场．若共赛了15场，则有几个球队参赛？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．如图是小强用八块相同的小立方块搭建的一个积木，他从左面看到的形状图是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．按图填空，并注明理由．

    （1）完成正确的证明：如图（1），已知AB∥CD，求证：∠BED=∠B+∠D
    证明：过E点作EF∥AB（经过直线外一点有且只有一条直线与这条直线平行）
    ∴∠1=∠B（两直线平行，内错角相等）
    ∵AB∥CD（已知）
    ∴EF∥CD（如果两条直线与同一直线平行，那么它们也平行）
    ∴∠2=∠D（两直线平行，内错角相等）
    又∠BED=∠1+∠2
    ∴∠BED=∠B+∠D （等量代换）．
    （2）如图（2），在△ABC中，EF∥AD，∠1=∠2，∠BAC=70°．将求∠AGD的过程填写完整．
    解：因为EF∥AD（已知）
    所以∠2=∠3．（两直线平行，同位相等）
    又因为∠1=∠2，所以∠1=∠3．（等量代换）
    所以AB∥DG（内错角相等，两直线平行）
    所以∠BAC+∠AGD=180° （两直线平行，同旁内角互补）．
    又因为∠BAC=70°，所以∠AGD=110°．

    查看答案和解析>>

    同步练习册答案