
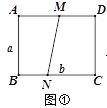
【题目】如图①,矩形纸片ABCD的边长分别为a、b(a<b),点M、N分别为边AD、BC上两点(点A、C除外),连接MN.
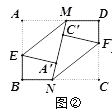
(1)如图②,分别沿ME、NF 将MN两侧纸片折叠,使点A、C分别落在MN上的A′、C′处,直接写出ME与FN的位置关系;
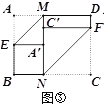
(2)如图③,当MN⊥BC 时,仍按(1)中的方式折叠,请求出四边形A′EBN与四边形C′FDM 的周长(用含a的代数式表示),并判断四边形A′EBN与四边形C′FDM周长之间的数量关系;
(3)如图④,若对角线BD与MN交于点O,分别沿BM、DN将MN两侧纸片折叠,折叠后,点A、C恰好都落在点O处,并且得到的四边形BNDM是菱形,请你探索a、b之间的数量关系.

【答案】(1)EM∥NF ;(2)![]() 的周长与
的周长与![]() 的周长相等;(3)
的周长相等;(3)![]()
【解析】(1)先根据翻折变换的性质得到∠EMN=![]() ∠AMN,∠FNC′=
∠AMN,∠FNC′=![]() ∠MNC,再由平行线的性质可得到∠AMN=∠MNC,由平行线的判定定理即可得到ME∥FN;
∠MNC,再由平行线的性质可得到∠AMN=∠MNC,由平行线的判定定理即可得到ME∥FN;
(2)由折叠得知:A′E=AE,根据四边形A′EBN是矩形,即可求出四边形A′EBN的即四边形C′FDM的周长;
(3)根据折叠的性质可知OD=CD=OB=a,在△BCD中利用勾股定理即可求出b的值.
(1)EM∥NF ;
(2)∵矩形ABCD,
∴∠A=90°=∠B,
∵△AEM沿EM折叠到△![]()
∴∠![]() ,AE=
,AE=![]()
∵MN⊥BC,
∴∠MNB=90°,
∴有矩形![]() ,
,
∴其周长为![]() ,
,
同理 四边形![]() 也为矩形,周长为,
也为矩形,周长为,
![]() ,
,
∴![]() 的周长与
的周长与![]() 的周长相等;
的周长相等;
(3)∵四边形BNDM是菱形,
∴BM=MD,BD⊥MN,BO=DO,MO=NO,∠MBO=∠NBO,
∵△ABM沿BM折叠到△OBM,
∴AB=OB,AM=MO,∠ABM=∠OBM,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴∠MBO=30°,
在Rt△MBO中,∠MOB=90°,
∴BM=2MO,
设MO=x,BM=2x,
BO=![]()
AD=AM+MD=BM+MO=3x
∴![]() ,即
,即![]() .
.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
【题目】定义:如图1,抛物线 ![]() 与
与 ![]() 轴交于A,B两点,点P在抛物线上(点P与A,B两点不重合),如果△ABP的三边满足
轴交于A,B两点,点P在抛物线上(点P与A,B两点不重合),如果△ABP的三边满足 ![]() ,则称点P为抛物线
,则称点P为抛物线 ![]() 的勾股点。
的勾股点。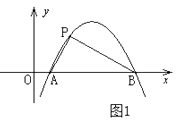
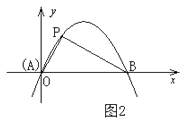
(1)直接写出抛物线 ![]() 的勾股点的坐标;
的勾股点的坐标;
(2)如图2,已知抛物线C: ![]() 与
与 ![]() 轴交于A,B两点,点P(1,
轴交于A,B两点,点P(1, ![]() )是抛物线C的勾股点,求抛物线C的函数表达式;
)是抛物线C的勾股点,求抛物线C的函数表达式;
(3)在(2)的条件下,点Q在抛物线C上,求满足条件 ![]() 的点Q(异于点P)的坐标
的点Q(异于点P)的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在全体丽水人民的努力下,我市剿灭劣V类水“河道清淤”工程取得了阶段性成果,下面的右表是全市十个县(市、区)指标任务数的统计表;左图是截止2017年3月31日和截止5月4日,全市十个县(市、区)指标任务累计完成数的统计图.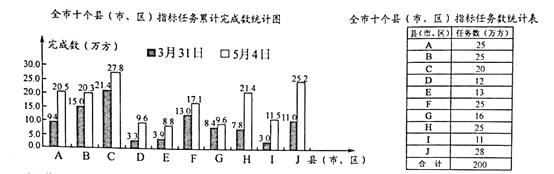
(1)截止3月31日,完成进度(完成进度=累计完成数÷任务数×100%)最快、电慢的县(市、区)分别是哪一个?
(2)求截止5月4日全市的完成进度;
(3)请结合图形信息和数据分析,对I且完成指标任务的行动过程和成果进行评价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠BAD=60°
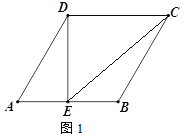
(1)如图1,点E为线段AB的中点,连接DE、CE,若AB=4,求线段EC的长;
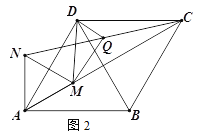
(2)如图2,M为线段AC上一点(不与A、C重合),以AM为边向上构造等边三角形AMN,连接NC、DM,Q为线段NC的中点,连接DQ、MQ,判断DM与DQ的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图A、B分别为数轴上的两点,A点对应的数为-10,B点对应的数为90.
![]()
(1)请写出与A,B两点距离相等的M点对应的数;
(2)现在有一只电子蚂蚁P从B点出发时,以3个单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以2个单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的C点相遇,求C点对应的数是多少.
(3)若当电子蚂蚁P从B点出发时,以3个单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以2个单位/秒的速度向右运动,求经过多长的时间两只电子蚂蚁在数轴上相距35个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据生物学研究结果,青春期男女生身高增长速度呈现如下图规律,由图可以判断,下列说法错误的是( ) 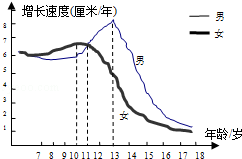
A.男生在13岁时身高增长速度最快
B.女生在10岁以后身高增长速度放慢
C.11岁时男女生身高增长速度基本相同
D.女生身高增长的速度总比男生慢
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上有A、B两点,所表示的数分别为n,n+6,A点以每秒5个单位长度的速度向右运动,同时B点以每秒3个单位长度的速度也向右运动,设运动时间为t 秒.
(1)当n=1时,求AB的值;
(2)当t 为何值时,A、B两点重合;
(3)在上述运动的过程中,若P为线段AB的中点,数轴上点C所表示的数为n+10是否存在t 的值,使得线段PC=4,若存在,求t 的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个自然数的立方,可以分裂成若干个连续奇数的和,例如:23,33和43分别可以按如图所示的方式“分裂”,则63“分裂”出的奇数中,最大的奇数是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com