
分析 (1)根据y1、y2图象间的关系结合y2的函数表达式,即可得出y1的表达式,进而可找出y1与y轴的交点和y2的顶点,根据点的坐标利用待定系数法即可求出y1的表达式;
(2)画出y2与y3的函数图象,观察图象,即可得出结论;
(3)根据y1、y2、y3的表达式,找出它们的单增区间,由此即可得出实数m的最大值.
解答 解:(1)∵y1向右平移2个单位,向上平移1个单位得到y2,
∴y2向左平移2个单位,向下平移1个单位得到y1,
∵y2=-x2+2x,
∴y1=-(x+2)2+2(x+2)-1,
∴y1的表达式为y1=-x2-2x-1,
∴y1与y轴的交点为(0,-1).
∵y2=-x2+2x=-(x-1)2+1,
∴y2的顶点坐标为(1,1).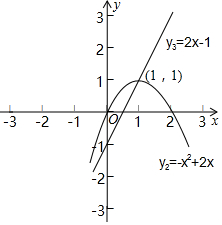
∵y3经过(0,-1)、(1,1),
∴$\left\{\begin{array}{l}{b=-1}\\{k+b=1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=2}\\{b=-1}\end{array}\right.$,
∴y3的表达式为y3=2x-1.
(2)依照题意,画出函数y2、y3的图象,如图所示.
观察函数图象,可得:
当0≤x<1时,y2>y3;
当x=1时,y2=y3;
当x>1时,y2<y3.
(3)∵y1=-x2-2x-1=-(x+1)2,y2=-(x-1)2+1,y3=2x-1,
∴y1在x≤-1时随x的增大而增大,y2在x≤1时随x的增大而增大,y3一直都随x的增大而增大,
∴m≤-1时,y1,y2,y3均随着x的增大而增大,
∴m的最大值为-1.
点评 本题考查了二次函数与不等式、待定系数法求一次函数解析式、二次(一次)函数图象以及二次函数的性质,解题的关键是:(1)利用平移找出y1的表达式;(2)画出函数图象,利用数形结合解决问题;(3)找出三个函数的单增区间.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
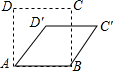 如图,若将长度相等的四根木条钉成的正方形木框ABCD变形成菱形ABC′D′的形状,并使∠BAD′=45°,则正方形ABCD的面积与菱形ABC′D′的面积之比为$\sqrt{2}$:1.
如图,若将长度相等的四根木条钉成的正方形木框ABCD变形成菱形ABC′D′的形状,并使∠BAD′=45°,则正方形ABCD的面积与菱形ABC′D′的面积之比为$\sqrt{2}$:1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com