
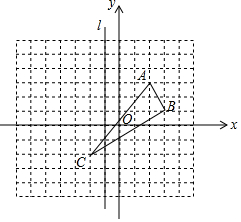
 如图,已知△ABC的三个顶点分别为A(2,3),B(3,1),C(-2,-2),直线l是经过(-1,0)且垂直于x轴的一条直线.
如图,已知△ABC的三个顶点分别为A(2,3),B(3,1),C(-2,-2),直线l是经过(-1,0)且垂直于x轴的一条直线.分析 (1)根据轴对称的性质得到△ABC的三个顶点的对称点,连接这些对称点,就得到原图形的轴对称图形;
(2)根据四边形ABED为梯形,运用面积公式即可得到四边形ABED的面积;
(3)根据点M(-5,a-2)与点N(b,2a-1)关于直线l成轴对称,可得两点到直线l的距离相等,两点到x轴的距离也相等,即可得出a与b的值.
解答 解:(1)如图所示,△DEF即为所求,D(-4,3),E(-5,1),F(0,-2);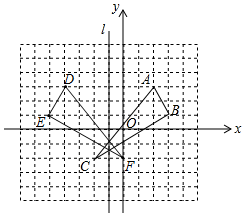
(2)四边形ABED的面积=$\frac{(6+8)×2}{2}$=14;
(3)∵点M(-5,a-2)与点N(b,2a-1)关于直线l成轴对称,
∴b-(-1)=-1-(-5),a-2=2a-1,
解得a=-1,b=3.
点评 本题主要考查了利用轴对称变换进行作图,解题时注意:画一个图形的轴对称图形时,是先从确定一些特殊的对称点开始的.


科目:初中数学 来源: 题型:选择题
 小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),若想配一块与原来大小一样的三角形玻璃?应该带( )去.
小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),若想配一块与原来大小一样的三角形玻璃?应该带( )去.| A. | 第1块 | B. | 第2块 | C. | 第3块 | D. | 第4块 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{16}$=±4 | B. | $\sqrt{(-2)^{2}}$=2 | C. | $\sqrt{27}$=3 | D. | $\frac{1}{\sqrt{3}}$=$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 22 | B. | 23 | C. | 27 | D. | 28 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com