
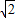 ,求m的值,并求出此时方程的两根.
,求m的值,并求出此时方程的两根. ”可以求得(x1-x2)2=(x1+x2)2-4x1x2=8,从而列出关于m的方程,通过解该方程即可求得m的值;最后将m值代入原方程并解方程.
”可以求得(x1-x2)2=(x1+x2)2-4x1x2=8,从而列出关于m的方程,通过解该方程即可求得m的值;最后将m值代入原方程并解方程. ∴(x1-x2)2=(2
∴(x1-x2)2=(2 )2
)2 ,x2=-
,x2=- …11分
…11分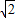 ,x2=-2-
,x2=-2- …12分
…12分

科目:初中数学 来源:第23章《一元二次方程》中考题集(23):23.3 实践与探索(解析版) 题型:解答题
 .
.查看答案和解析>>
科目:初中数学 来源:2007年全国中考数学试题汇编《一元二次方程》(04)(解析版) 题型:解答题
 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com