
【题目】如图,在菱形ABCD中,E是AB的中点,且DE⊥AB,AB=10,则∠ABC= , 对角线AC的长为 . 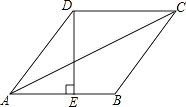
【答案】120°;10 ![]()
【解析】解:∵四边形ABCD是菱形,
∴AB=BC=CD=DA,AD∥BC,
∵E是AB的中点,且DE⊥AB,
∴AE= ![]() AD,
AD,
∴sin∠ADE= ![]() ,
,
∴∠ADE=30°,
∴∠DAE=60°,
∵AD∥BC,
∴∠ABC=180°﹣60°=120°;
连接BD,交AC于点O,
在菱形ABCD中,∠DAE=60°,
∴∠CAE=30°,AB=10,
∴OB=5,
根据勾股定理可得:AO= ![]() =5
=5 ![]() ,
,
即AC=10 ![]() .
.
所以答案是:120°;10 ![]() .
.
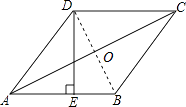
【考点精析】本题主要考查了线段垂直平分线的性质和菱形的性质的相关知识点,需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】阅读材料:求1+2+22+23+24+…+22013的值.
解:设S=1+2+22+23+24+…+22012+22013,将等式两边同时乘以2得:
2S=2+22+23+24+25+…+22013+22014
将下式减去上式得2S﹣S=22014﹣1
即S=22014﹣1
即1+2+22+23+24+…+22013=22014﹣1
请你仿照此法计算:
(1)1+2+22+23+24+…+210
(2)1+3+32+33+34+…+3n(其中n为正整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB、CD、EF相交于点O,EF⊥AB,OG为∠COF的平分线,OH为∠DOG的平分线.
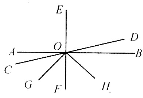
(1)若∠AOC∶∠COG=4∶7,求∠DOF的大小;
(2)若∠AOC∶∠DOH=8∶29,求∠COH的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)已知二次函数![]() .
.
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2-2x-3与x轴交于A、B两点.
(1)当0<x<3时,求y的取值范围;
(2)点P为抛物线上一点,若S△PAB=10,求出此时点P的坐标.

五、解答题(本大题3小题,每小题9分,共27分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商店运来120台洗衣机,每台售价是440元,每售出一台可以得到售价15%的利润,其中两台有些破损,按售价打八折出售。这批洗衣机售完后实得利润为_________元;
查看答案和解析>>
科目:初中数学 来源: 题型:
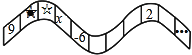
【题目】如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
(![]() )可求得
)可求得![]() __________,第
__________,第![]() 个格子中的数为__________.
个格子中的数为__________.
(![]() )判断:前
)判断:前![]() 个格子中所填整数之和是否可能为
个格子中所填整数之和是否可能为![]() ?若能,求出
?若能,求出![]() 的值,若不能,请说明理由.
的值,若不能,请说明理由.
(![]() )若取前
)若取前![]() 格子中的任意两个数记作
格子中的任意两个数记作![]() 、
、![]() ,且
,且![]() ,那么所有的
,那么所有的![]() 的和可以通过计算
的和可以通过计算![]() 得到,其结果为__________;若
得到,其结果为__________;若![]() 、
、![]() 为前
为前![]() 格子中的任意两个数记作
格子中的任意两个数记作![]() 、
、![]() ,且
,且![]() ,则所有的
,则所有的![]() 的和为__________.
的和为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com