
在△ABC中,AB、BC、AC三边的长分别为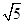 、
、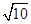 、
、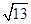 ,求这个三角形的面积.
,求这个三角形的面积.
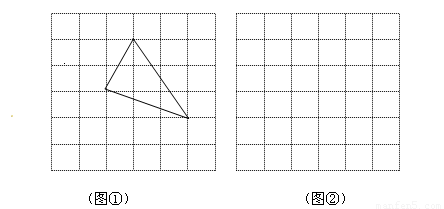
小华同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样就不需要求△ABC的高,而借用网格就能计算出它的面积.(本题8分)
⑴ 请你将△ABC的面积直接填写在横线上.
思维拓展:
⑵ 我们把上述求△ABC面积的方法叫做构图法.若△ABC三边的长分别为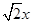 、
、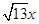 、
、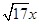 (
(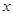 >0),请利用图②的正方形网格(每个小正方形的边长为
>0),请利用图②的正方形网格(每个小正方形的边长为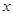 )画出相应的△ABC,并求出它的面积.
)画出相应的△ABC,并求出它的面积.
探索创新:
⑶ 若△ABC三边的长分别为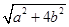 、
、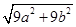 、
、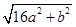 (
(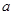 >0,
>0,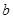 >0,且
>0,且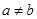 ),试运用构图法求出这个三角形的面积.
),试运用构图法求出这个三角形的面积.
科目:初中数学 来源: 题型:
 (2013•宁德质检)如图,在△ABC中,AB=AC=6,点0为AC的中点,OE⊥AB于点E,OE=
(2013•宁德质检)如图,在△ABC中,AB=AC=6,点0为AC的中点,OE⊥AB于点E,OE=| 3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•襄阳)如图,在△ABC中,AB=AC,AD⊥BC于点D,将△ADC绕点A顺时针旋转,使AC与AB重合,点D落在点E处,AE的延长线交CB的延长线于点M,EB的延长线交AD的延长线于点N.
(2012•襄阳)如图,在△ABC中,AB=AC,AD⊥BC于点D,将△ADC绕点A顺时针旋转,使AC与AB重合,点D落在点E处,AE的延长线交CB的延长线于点M,EB的延长线交AD的延长线于点N.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•吉林)如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作?ABDE,连接AD,EC.
(2012•吉林)如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作?ABDE,连接AD,EC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com