在平面直角坐标系中,点O为坐标原点.
(1)若点P的坐标为(1,2),将线段OP绕原点O逆时针旋转90°得到线段OQ,则点Q的坐标为______.
(2)若过点P的直线L1的函数解析式为y=2x,求过点P且与直线L1垂直的直线L2的函数解析式;
(3)若直线L1的函数解析式为y=x+4,直线L2的函数解析式为y=-x-2,求证:直线L1与直线L2互相垂直;
(4)设直线L1的函数关系式为y=k1x+b1,直线L2的函数关系式为y=k2x+b2(k1•k2≠0).根据以上的解题结论,请你用一句话来总结概括:直线L1和直线L2互相垂直与k1、k2的关系.
(5)请运用(4)中的结论来解决下面的问题:
在平面直角坐标系中,点A的坐标为(-3,-6),点B的坐标为(7,2),求线段AB的垂直平分线的函数解析式.
【答案】
分析:(1)由坐标转换可知,逆时针旋转90°,坐标互换,纵坐标变号.
(2)过点P的直线L
1的函数解析式为y=2x,与x轴成α角,即tanα=2,与直线L
1垂直的直线L
2的函数解析式为y=kx+b,即tanβ=k,又两直线垂直,故其夹角为90°,即tan(β-α)=[tanβ-tanα]/[1+tanα tanβ]=0.且P(1,2),代入方程,即可得出.
(3)设两函数与x轴的夹角分别为a,b,即tana=1,tanb=-1,代入tan(b-a)=[tanb-tana]/[1+tana tanb]即可.
(4)直线L
1和直线L
2互相垂直,k
1×k
2=-1.
(5)由两点式可知两点所在直线的斜率,根据(4)的结论以及A、B的中点坐标即可得出函数解析式.
解答:解:(1)由坐标转换可知,Q(-2,1).
(2)直线L
1:y=2x,即tanα=2,设直线L
2的函数解析式为y=kx+b,即tanβ=k,
又两直线垂直,tan(β-α)=[tanβ-tanα]/[1+tanα tanβ],所以tana tanb=-1,即2k=-1,
即k=

,
又因为直线L
2过点P,
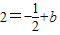
,
得b=

,
故直线L
2的函数解析式为:
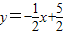
.
(3)设直线L
1、直线L
2与x轴的夹角分别为a,b,即tana=1,tanb=-1,
代入tan(b-a)=[tanb-tana]/[1+tana tanb],可知1+tana tanb=0;即tan(b-a)无意义,
即两直线夹角为90°,即证直线L
1与直线L
2互相垂直;
(4)直线L
1和直线L
2互相垂直,k
1×k
2=-1.
(5)设线段AB的垂直平分线的函数解析式为y=kx+b.
由(4)可知
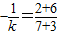
,即k=-

,又过AB的中点(2,-2),代入函数式,可得b=

,即线段AB的垂直平分线的函数解析式为y=
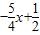
.
点评:本题着重考查了学生对直线互相垂直时两斜率之积为-1的证明,要求学生对此类题熟练掌握.

 ,
,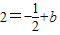 ,
, ,
,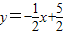 .
.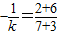 ,即k=-
,即k=- ,又过AB的中点(2,-2),代入函数式,可得b=
,又过AB的中点(2,-2),代入函数式,可得b= ,即线段AB的垂直平分线的函数解析式为y=
,即线段AB的垂直平分线的函数解析式为y=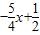 .
.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB= 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.