
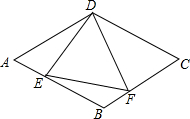
 如图,菱形ABCD中,AB=6,∠A=60°,点E是线段AB上一点(不与A,B重合),作∠EDF交BC于点F,且∠EDF=60°.
如图,菱形ABCD中,AB=6,∠A=60°,点E是线段AB上一点(不与A,B重合),作∠EDF交BC于点F,且∠EDF=60°.分析 (1)先求得菱形的两条对角线的长度,然后根据菱形的面积等于两对角线乘积的一半求解即可;
(2)①连接BD,证明△ADE≌△BDF,从而可得到ED=DF,由因为∠EDF=60°,所以三角形DEF为等边三角形;
②由△ADE≌△BDF可知:S△ADE=S△BDF,所以四边形的面积=△EDB的面积+△DBF的面积=△EDB的面积+△DAE的面积=菱形面积的一半;
③由△ADE≌△BDF可知:BF=AE,所以BF+BE=AE+BE=6,所以当ED和DF最短时,四边形的周长最小,然后由垂线段最短可知当DE⊥AB时,DE最短,然后在Rt△ADE中即可求得DE的长,从而可求得四边形周长的最小值.
解答 解:(1)连接BD、AC.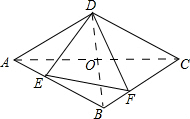
∵四边形ABCD是菱形,
∴AD=AB,AC⊥BD,∠DAO=$\frac{1}{2}$∠A=30°.
∵AD=AB,∠A=60°,
∴△ABD为等边三角形.
∴BD=AD=AB=6.
∵在Rt△ADO中,∠DAO=30°,
∴OD=$\frac{1}{2}$AD=3,AO=$\sqrt{A{D}^{2}-O{D}^{2}}=\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$.
∴AC=6$\sqrt{3}$.
∴菱形ABCD的面积=$\frac{1}{2}×AC×BD$=$\frac{1}{2}×6\sqrt{3}×6$=18$\sqrt{3}$.
(2)①由(1)可知:△ABD为等边三角形.
∴AD=BD,∠ADB=60°.
∵∠ADE+∠EDB=60°,∠FDB+∠EDB=60°,
∴∠ADE=∠FDB.
∵四边形ABCD是菱形,∠A=60°,
∴∠DBF=$\frac{1}{2}$∠ABC=$\frac{1}{2}×120°=60°$.
∴∠DAE=∠DBF.
在△DAE和△DBF中,
$\left\{\begin{array}{l}{∠ADE=∠BDF}\\{AD=DF}\\{∠DAE=∠DBF}\end{array}\right.$,
∴△DAE≌△DBF.
∴DE=DF.
又∵∠EDF=60°
∴△EDF为等边三角形.
②四边形DEBF的面积=9$\sqrt{3}$.
理由:∵△DAE≌△DBF.
∴S△ADE=S△BDF,
∴四边形DEBF的面积=△EDB的面积+△DBF的面积=△EDB的面积+△DAE的面积=$\frac{1}{2}$×菱形ABCD的面积=$\frac{1}{2}×18\sqrt{3}=9\sqrt{3}$.
③∵△DAE≌△DBF.
∴BF=AE.
∴BF+BE=AE+BE=AB=6.
∴当ED、DF有最小值时,四边形的周长最短.
由垂线最短,可知当DE⊥AB时,ED、DF最短.
在Et△ADE中,∠DAE=60°,
∴sin60°=$\frac{DE}{AD}=\frac{\sqrt{3}}{2}$.
∴DE=$\frac{\sqrt{3}}{2}×6$=3$\sqrt{3}$.
∴四边形DEBF的周长的最小值=DE+DF+BE+BF=DE+DF+AB=3$\sqrt{3}$+3$\sqrt{3}$+6=6$\sqrt{3}$+6.
点评 本题主要考查的是菱形的性质,解答本题需要同学们熟练掌握菱形的性质和全等三角形的性质和判定,证得△DAE≌△DBF是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
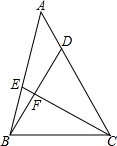 如图,在△ABC中,点D,E分别在边AC,AB上,且BD=CE=BC.若∠A=25°,则∠BFC=130°;若∠A=45°且BF:CF=5:12,则AE:AB=2:3.
如图,在△ABC中,点D,E分别在边AC,AB上,且BD=CE=BC.若∠A=25°,则∠BFC=130°;若∠A=45°且BF:CF=5:12,则AE:AB=2:3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
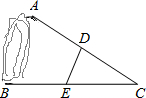
 有一张一个角为30°,最小变长为4的直角三角形纸片,沿图中所示的中位线剪开后,将两部分拼成一个四边形,所得四边形的周长是8+4$\sqrt{3}$或16.
有一张一个角为30°,最小变长为4的直角三角形纸片,沿图中所示的中位线剪开后,将两部分拼成一个四边形,所得四边形的周长是8+4$\sqrt{3}$或16.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠ACB=90°,AC=BC=4,点D为BC边的中点,将△ABC绕点D逆时针旋转45度,得到△A′B′C′,B′C′与AB交于点E,则图中阴影部分四边形ACDE的面积为( )
如图,在Rt△ABC中,∠ACB=90°,AC=BC=4,点D为BC边的中点,将△ABC绕点D逆时针旋转45度,得到△A′B′C′,B′C′与AB交于点E,则图中阴影部分四边形ACDE的面积为( )| A. | 6 | B. | 7 | C. | 8 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,A,B两点被池塘隔开,在AB外选一点C,连接AC和BC,通过测量分别取AC,BC的中点D和E,量得DE长210米,则A,B两点间的距离为( )
如图,A,B两点被池塘隔开,在AB外选一点C,连接AC和BC,通过测量分别取AC,BC的中点D和E,量得DE长210米,则A,B两点间的距离为( )| A. | 280米 | B. | 300米 | C. | 420米 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com