
【题目】如图,正方形ABCD的边长为4,E为BC上的一点,BE=1,F为AB的中点,P为AC上一个动点,则PF+PE的最小值为( )
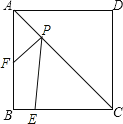
A. 2![]() B. 4 C.
B. 4 C. ![]() D. 2
D. 2![]()
【答案】C
【解析】分析:
如下图,作点E关于直线AC的对称点E′,连接E′F,则E′F的长即为所求的PE+PF的最小值,过F作FG⊥CD于G,则CE′=CE=BC-BE=3,CG=BF=2,FG=BC=4,由此可得GE′=1,这样在Rt△FGE′中由勾股定理求出FE′的长即可.
详解:
作点E关于直线AC的对称点E′,连接E′F,则E′F的长即为所求的PE+PF的最小值,
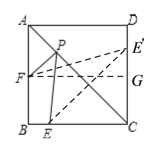
过F作FG⊥CD于G,则由题意可得CE′=CE,CG=BF,FG=BC,
∵BC=AB=4,BE=1,点F是AB的中点,
∴CE′=CE=BC-BE=3,CG=FB=2,FG=BC=4,
∴GE′=CE′-CG=3-2=1,
∴在Rt△E′FG中,E′F=![]() .
.
故选C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】地球运动是同学们非常喜欢的日常体育运动,为了更合理地配置体育运动器材和场地,某校针对“你最喜欢的球类运动”进行了一次随机抽样调查(每名被调查者分别选一项球类运动),并把调查结果绘制成如图的两个统计图表(不完整).
某校学生最喜爱的球类运动统计表
最喜爱的球类运动 | 人数 |
足球 | 27 |
篮球 |
|
乒乓球 | 24 |
羽毛球 | 24 |
排球 |
|
某校学生最喜爱的球类运动统计图

请根据所给信息,解答下列问题:
(1)本次被抽样调查的学生共有多少人?
(2)求扇形统计图中最喜爱篮球部分的圆心角度数;
(3)若该校共有学生960人,请根据抽样结果估计学生中最喜爱乒乓球的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy(如图)中,已知抛物线y=![]() +bx+c点经过A(1,0)、B(0,2).
+bx+c点经过A(1,0)、B(0,2).
(1)求该抛物线的表达式;
(2)设该抛物线的对称轴与x轴的交点为C,第四象限内的点D在该抛物线的对称轴上,如果以点A、C、D所组成的三角形与△AOB相似,求点D的坐标;
(3)设点E在该抛物线的对称轴上,它的纵坐标是1,联结AE、BE,求sin∠ABE.
查看答案和解析>>
科目:初中数学 来源: 题型:
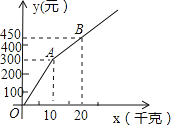
【题目】“莓好莒南 幸福家园”---2018年莒南县第三届草莓旅游文化节期间,甲、乙两家草莓采摘园草莓品质相同,销售价格也相同,均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买60元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘的草莓超过一定数量后,超过部分打折优惠,优惠期间,设某游客的草莓采摘量为![]() 千克
千克![]() ,在甲采摘园所需总费用为
,在甲采摘园所需总费用为![]() 元
元![]() ,在乙采摘园所需总费用为
,在乙采摘园所需总费用为![]() 元
元![]() ,图中折线OAB表示
,图中折线OAB表示![]() 与x之间的函数关系.
与x之间的函数关系.
![]() 求
求![]() ,
,![]() 与x的函数表达式;
与x的函数表达式;
![]() 若选择甲采摘园所需总费用较少,请求出草莓采摘量x的范围.
若选择甲采摘园所需总费用较少,请求出草莓采摘量x的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=2,将线段CD绕点C顺时针旋转90°得到线段CE,线段BD绕点B顺时针旋转90°得到线段BF,连接BF,则图中阴影部分的面积是_____.
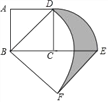
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在横线上完成下面的证明,并在括号内注明理由.
已知:如图,∠ABC+∠BGD=180°,∠1=∠2.
求证:EF∥DB.
证明:∵∠ABC+∠BGD=180°,(已知)
∴ .( )
∴∠1=∠3.( )
又∵∠1=∠2,(已知)
∴ .( )
∴EF∥DB.( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在每个小正方形的边长为1的网格中,有以AB为直径的半圆和线段AP,AB组成的一个封闭图形,点A,B,P都在网格点上.
(Ⅰ)计算这个图形的面积为_____;
(Ⅱ)请在如图所示的网格中,用无刻度的直尺,画出一条能够将这个图形的面积平分的直线,并简要说明这条直线是如何找到的(不要求证明)_____.
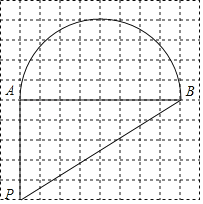
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:b是最小的正整数,且a、b满足(c﹣6)2+|a+b|=0,请回答问题
(1)请直接写出a、b、c的值.a= ,b= ,c=
(2)a、b、c所对应的点分别为A、B、C,点P为一动点,其对应的数为x,点P在A、B之间运动时,请化简式子:|x+1|﹣|x﹣1|﹣2|x+5|(请写出化简过程)
![]()
(3)在(1)(2)的条件下,点A、B、C开始在数轴上运动,若点A以每秒n(n>0)个单位长度的速度向左运动,同时,点B和点C分别以每秒2n个单位长度和5n个单位长度的速度向右运动,假设经过t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC﹣AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为厉行节能减排,倡导绿色出行,今年3月以来.“共享单车”(俗称“小黄车”)公益活动登陆我市中心城区,某公司拟在甲、乙两个街道社区投放一批“小黄车”,这批自行车包括A、B两种不同款型,请回答下列问题:
问题1:单价
该公司早期在甲街区进行了试点投放,共投放A、B两型自行车各50辆,投放成本共计7500元,其中B型车的成本单价比A型车高10元,A、B两型自行车的单价各是多少?
问题2:投放方式
该公司决定采取如下投放方式:甲街区每1000人投放a辆“小黄车”,乙街区每1000人投放![]() 辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com