
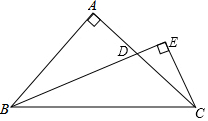
 已知等腰直角三角形ABC,BC是斜边,∠B的平分线交AC于D,过C作CE与BD垂直且交BD延长线于E.已知CE=4,则BD的长为( )
已知等腰直角三角形ABC,BC是斜边,∠B的平分线交AC于D,过C作CE与BD垂直且交BD延长线于E.已知CE=4,则BD的长为( )| A. | 5 | B. | 8 | C. | $\sqrt{73}$ | D. | 7 |
分析 延长CE,BA交于一点F,由已知条件可证得△BFE全≌△BEC,所以FE=EC,即CF=2CE,再通过证明△ADB≌△FAC可得FC=BD,所以BD=2CE.
解答  证明:如图,分别延长CE,BA交于一点F.
证明:如图,分别延长CE,BA交于一点F.
∵BE⊥EC,
∴∠FEB=∠CEB=90°,
∵BE平分∠ABC,
∴∠FBE=∠CBE,
又∵BE=BE,
∴△BFE≌△BCE (ASA).
∴FE=CE.
∴CF=2CE.
∵AB=AC,∠BAC=90°,∠ABD+∠ADB=90°,∠ADB=∠EDC,
∴∠ABD+∠EDC=90°.
又∵∠DEC=90°,∠EDC+∠ECD=90°,
∴∠FCA=∠DBC=∠ABD.
∴△ADB≌△AFC.
∴FC=DB,
∴BD=2EC=8.
故选B.
点评 本题考查了全等三角形的判断和性质,等腰直角三角形的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
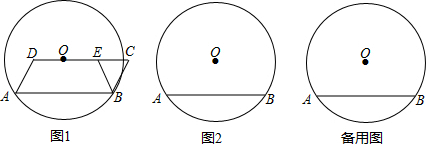
 如图,是由边长为1的小正方形组成的正方形网格,设顶点在这些小正方形顶点的三角形为格点三角形,图中已给出△ABC的一边AB的位置.
如图,是由边长为1的小正方形组成的正方形网格,设顶点在这些小正方形顶点的三角形为格点三角形,图中已给出△ABC的一边AB的位置.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
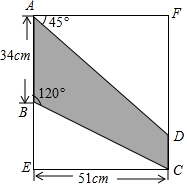 2016年11月6日,第十一届中国国际航空航天博览会(珠海航展)圆满落幕.从运-20、歼-10B、轰-6K、空警-500、武直-10K等主力战机与观众的零距离接触,到长剑、鹰击、红旗等导弹家族的系列化呈现,再到翼龙无人机等新型装备的集体亮相,中国空军用看得见、摸得着的“真家伙”,向观众展现了中国空军前所未有的强大自信.慧慧想在一个矩形材料中剪出如图所示的阴影图形,作为要制作的航模飞机的一个翅膀,请你根据图中数据帮她计算出 BE,CD 的长度(结果保留整数,参考数据:$\sqrt{3}$≈1.7)
2016年11月6日,第十一届中国国际航空航天博览会(珠海航展)圆满落幕.从运-20、歼-10B、轰-6K、空警-500、武直-10K等主力战机与观众的零距离接触,到长剑、鹰击、红旗等导弹家族的系列化呈现,再到翼龙无人机等新型装备的集体亮相,中国空军用看得见、摸得着的“真家伙”,向观众展现了中国空军前所未有的强大自信.慧慧想在一个矩形材料中剪出如图所示的阴影图形,作为要制作的航模飞机的一个翅膀,请你根据图中数据帮她计算出 BE,CD 的长度(结果保留整数,参考数据:$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,设点P在函数y=$\frac{6}{x}$的图象上,PC⊥x轴于点C,交函数y=$\frac{2}{x}$的图象于点A,PD⊥y轴于点D,交函数y=$\frac{2}{x}$的图象于点B,则四边形PAOB的面积为4.
如图,设点P在函数y=$\frac{6}{x}$的图象上,PC⊥x轴于点C,交函数y=$\frac{2}{x}$的图象于点A,PD⊥y轴于点D,交函数y=$\frac{2}{x}$的图象于点B,则四边形PAOB的面积为4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com