Question

【题目】在平面直角坐标系xOy中，给出如下定义：

对于⊙C及⊙C外一点P，M，N是⊙C上两点，当∠MPN最大，称∠MPN为点P关于⊙C的“视角”．直线l与⊙C相离，点Q在直线l上运动，当点Q关于⊙C的“视角”最大时，则称这个最大的“视角”为直线l关于⊙C的“视角”．

（1）如图，⊙O的半径为1，

①已知点A（1，1），直接写出点A关于⊙O的“视角”；已知直线y = 2，直接写出直线y = 2关于⊙O的“视角”；

②若点B关于⊙O的“视角”为60°，直接写出一个符合条件的B点坐标；

（2）⊙C的半径为1，

①C的坐标为（1，2），直线l: y=kx + b（k > 0）经过点D（，0），若直线l关于⊙C的“视角”为60°，求k的值；

②圆心C在x轴正半轴上运动，若直线y =x +关于⊙C的“视角”大于120°，直接写出圆心C的横坐标xC的取值范围．

Answer 1

【答案】（1）① 90，60；②本题答案不唯一，如：B (0，2)；（3）.

【解析】试题分析：

（1）由题意可知，点P关于⊙O的“视角”是指从点P引出两条射线，当两条射线和⊙O相切时，两条射线所形成的的夹角就是点P关于⊙O的“视角”；直线关于⊙O的“视角”是指当直线与⊙O相离时，直线上的点Q距离圆心O最近时，点Q关于⊙O的“视角”就是直线关于⊙O的“视角”；由此可根据已知条件解答第一问；

（2）①由题意可知，若直线l关于⊙C的“视角”为60°，则说明在直线上存在一点P距离点C最近，且点P关于⊙C的“视角”为60°，则此时点P是与以点C为圆心，2为半径的圆相切的切点，如图1，过点C作CH⊥轴于点H，PE⊥轴于点E，由已知分析可得DP=DH=，∠PDE=60°，在△PDE中可求得DE和PE的长，得到点P的坐标，把P、D的坐标代入直线的解析式可求得k的值；

②如图2，由已知易得直线与轴相交于点A（-1，0），与轴相交于点B（0， ），若此时直线关于⊙C的视角∠EPF=120°，由已知条件求得OC的长，可得点C的坐标；如图3，当沿着轴向左移动时，直线关于⊙C的视角会变大，当直线和⊙C相切于点P时，由已知条件可求得OC的长，可得此时点C的坐标；综合起来可得的取值范围.

试题解析：

（1）①如下图，当点A的坐标为（1，1）时，易得点A关于⊙O的视角为90°；

∵直线y=2上距离圆心O最近的点是直线y=2与y轴的交点P，过点P作⊙O的两条切线PC、PD，切点为C、D，则直线y=2关于⊙O的视角是∠CPD，连接OD，由已知条件可求得∠OPD=30°，∴∠CPD=60°，即直线y=2关于⊙O的视角为60°.

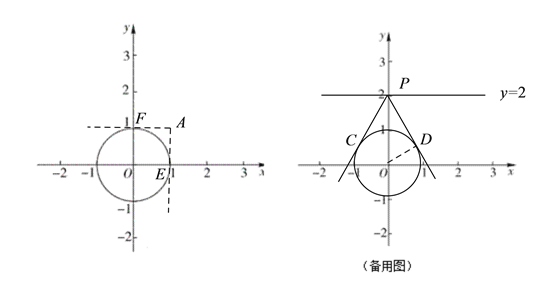
②由①中第2小问可知，满足条件的点B在以O为圆心，2为半径的圆上，这样的点很多，比如说点B（0，2）.

（2）①∵直线l: y=kx + b（k > 0）经过点D（，0），

∴.

∴.

∴直线l: .

设点P在直线上，若点P关于⊙C的“视角”为60°，则点P在以C为圆心，2为半径的圆上．

∵直线l关于⊙C的 “视角”为60°，

∴此时，点P是直线l上与圆心C的距离最短的点.

∴CP⊥直线l.

即直线l是以C为圆心，2为半径的圆的一条切线，如图1所示．

作过点C作CH⊥轴于点H，PE⊥轴于点E，

∴点H的坐标为（1，0），

又∵点D的坐标为，

∴DH ==PD．

∴tan∠CDH=，

∴∠CDH=30°，∠PDH=60°，

∴DE=PDcos60°=，PE= PDsin60°=3，

∴OE=DH-DE-OH=，

∴点P的坐标（，3）．

把点P的坐标代入l: ，解得： k=．

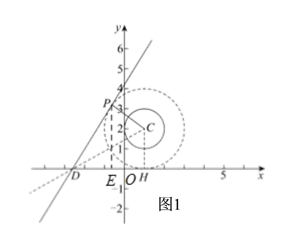
②如图2，由已知易得直线与轴相交于点A（-1，0），与轴相交于点B（0， ），

若此时直线关于⊙C的视角∠EPF=120°，

则∠EPC=60°，∠PEC=90°，CE=1，∴∠PCE=30°，

∴PC=，AC=，

∴OC=AC-OA=，

∴此时=；

如图3，当沿着轴向左移动时，直线关于⊙C的视角会变大，当直线和⊙C相切于点P时，连接CP，

∵在△ABO中，AO=1，BO=，

∴tan∠BAO=，

∴∠BAO=60°，

∴AC=，

∴OC=AC-OA=，

∴此时=，

综上所述， 的取值范围为： .