
 甲车从A地出发,途径C地时休息一小时,然后按原速度继续前进到达B地;乙车从C地出发到B地后又按原速返回C地,两车同时出发,并以各自的速度匀速行驶,设A,C,B在同一条直线上,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.
甲车从A地出发,途径C地时休息一小时,然后按原速度继续前进到达B地;乙车从C地出发到B地后又按原速返回C地,两车同时出发,并以各自的速度匀速行驶,设A,C,B在同一条直线上,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.分析 (1)根据甲车休息1小时列式求出m,根据甲的速度列式求出从C地到达B地行驶的时间,再加上休息的2.5小时即可得到n的值;
(2)利用待定系数法求一次函数解析式解答;
(3)求出乙车的速度,然后分:①相遇前两人的路程之和加上相距的60千米等于120千米列出方程求解即可;②相遇后,两人行驶的路程之和等120千米加60千米,列出方程求解即可.
解答 解:(1)∵甲车途经C地时休息一小时,
∴2.5-m=1,
∴m=1.5,
甲车的速度=$\frac{300-120}{1.5}$=120,
n=2.5+$\frac{120}{120}$=2.5+1=3.5
所以m=1.5,n=3.5;
(2)设甲车从C地到B地时的y与x的函数关系式为y=kx+b(k≠0),
因为函数图象经过(2.5,120)和(3.5,0),
所以,$\left\{\begin{array}{l}{2.5k+b=120}\\{3.5k+b=0}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{k=-120}\\{b=420}\end{array}\right.$,
所以,y=-120x+420(2.5≤x≤3.5).
设乙车从C地到B地时的y与x的函数关系式为y=k′x+b′(k′≠0),
因为函数图象经过(0,120)和(2,0),
所以,$\left\{\begin{array}{l}{b′=120}\\{2k′+b′=0}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{k′=-60}\\{b′=120}\end{array}\right.$,
所以,y=-60x+120(0≤x≤2).
(3)设两车相距60千米时,乙车行驶了x小时,
乙车的速度为:120÷2=60千米/时,
①若相遇前,则120(x-2.5)+60(x-2)=120-60,
解得x=$\frac{8}{3}$,
②若相遇后,则120(x-2.5)+60(x-2)=120+60,
解得x=$\frac{10}{3}$.
所以,两车相距60千米时,乙车行驶了$\frac{8}{3}$小时或$\frac{10}{3}$小时.
点评 本题考查了一次函数的应用,主要利用了待定系数法求一次函数解析式,路程、速度、时间三者之间的关系,根据休息1小时求出m的值是本题的突破口,(3)要注意分两种情况讨论.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 一个残破的车轮如图所示,测得它所剩圆弧两端点间的距离a=60cm,弧的中点到弧所对的弦的距离h=10cm,如果需要加工与原来大小相同的车轮,那么这个车轮的半径是多少?
一个残破的车轮如图所示,测得它所剩圆弧两端点间的距离a=60cm,弧的中点到弧所对的弦的距离h=10cm,如果需要加工与原来大小相同的车轮,那么这个车轮的半径是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
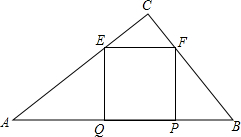 如图,在直角△ABC中,∠ACB=90°,若AC=40,BC=30,正方形EFPQ的一边QP在斜边AB上,C,F分别在AC、BC上,则该正方形的面积为$\frac{360000}{1369}$.
如图,在直角△ABC中,∠ACB=90°,若AC=40,BC=30,正方形EFPQ的一边QP在斜边AB上,C,F分别在AC、BC上,则该正方形的面积为$\frac{360000}{1369}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com