【题目】某商场将某种商品的售价从原来的每件
元经两次调价后调至每件
元．
（1）若该商店两次调价的降价率相同，求这个降价率；
（2）经调查，该商品每降价
元，即可多销售
件．若该商品原来每月可销售
件，那么两次调价后，每月可销售该商品多少件？
期末宝典单元检测分类复习卷系列答案科目：初中数学 来源： 题型：
【题目】为丰富学生的校园文化生活，珠海第十中学举办了“十中好声音”才艺比赛，三个年级都有男、女各一名选手进入决赛．初一年级选手编号为男1号、女1号，初二年级选手编号为男2号、女2号，初三年级选手编号为男3号、女3号．比赛规则是男、女各一名选手组成搭档展示才艺．
（1）用列举法说明所有可能出现搭挡的结果；
（2）求同一年级男、女选手组成搭档的概率；
（3）求高年级男选手与低年级女选手组成搭档的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
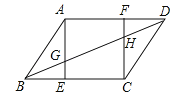
【题目】如图，在平行四边形ABCD中，AE⊥BC，CF⊥AD，垂足分别为E，F，AE，CF分别与BD交于点G和H，且AB=
．
（1）若tan∠ABE =2，求CF的长；
（2）求证：BG=DH．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将一块含30°角的直角三角板OAB和一块等腰直角三角板ODC按如图的方式放置在平面直角坐标系中．已知C、B两点分别在x轴和y轴上，∠ABO=∠D=90°，OB=OC，AB=3．
（1）求边OC的长．
（2）将直角三角板OAB绕点顺时针方向旋转，使OA落在x轴上的OA′位置，求图中阴影部分的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（问题情境）如图
，
中，
，
，我们可以利用
与
相似证明
，这个结论我们称之为射影定理，试证明这个定理；
（结论运用）如图
，正方形
的边长为
，点
是对角线
、
的交点，点
在
上，过点
作
，垂足为
，连接
，
（1）试利用射影定理证明
；
（2）若
，求的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
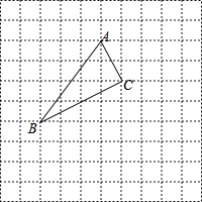
【题目】 如图，把△ABC放置在每个小正方形边长为1的网格中，点A，B，C均在格点上，建立适当的平面直角坐标系xOy，使点A（1，4），△ABC与△A'B'C'关于y轴对称．
（1）画出该平面直角坐标系与△A'B'C'；
（2）在y轴上找点P，使PC+PB'的值最小，求点P的坐标与PC+PB'的最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
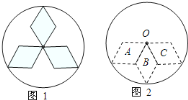
【题目】如图
所示，某产品的标志图案，要在所给的图形图
中，把
，
，
三个菱形通过一种或几种变换，使之变为与图一样的图案：
（1）请你在图中作出变换后的图案（最终图案用实线表示）；
（2）你所用的变换方法是________（在以下变换方法中，选择一种正
确的填到横线上，也可以用自己的话表述）．
①将菱形向上平移；
②将菱形绕点
旋转
；
③将菱形绕点旋转
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙、丙、丁四人做传球游戏：第一次由甲将球随机传给乙、丙、丁的某一人，从第二次起，每一次都由持球者将球再随机传给其他三人的某一人．
（1）求第二次传球后球回到甲手里的概率．
（2）如果甲跟另外n（n≥2）个人做（1）同样的游戏，那么，第三次传球后球回到甲手里的概率是 .（请用含n的式子直接写结果）．
查看答案和解析>>
科目：初中数学 来源： 题型：
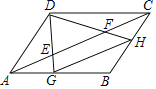
【题目】如图，E，F是平行四边形ABCD对角线AC上两点，AE=CF=
AC．连接DE，DF并延长，分别交AB，BC于点G，H，连接GH，则
的值为（ ）
A. 
B. 
C. 
D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
